Énoncé du problème
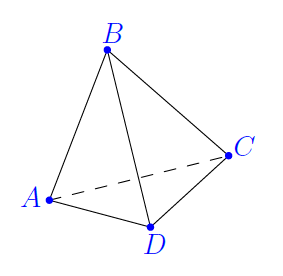
Une fourmi peut rentrer ou sortir dans un piège par le point A. Quand elle est à un sommet, elle choisit au hasard une des trois arêtes qui passent par ce sommet.
La fourmi est vivante si elle retourne au point A en ayant parcouru au plus 4 arêtes.
Sa chance de survie est-elle supérieur ou inférieure à une chance sur deux ?
Essaye d'estimer sa chance de survie.
Variante :
On peut choisir un autre polyèdre sur lequel se déplacerait la fourmi.
Choix du problème
Compétences transversales
♦ Former les élèves à la pensée statistique et aux phénomènes aléatoires.
♦ Construire des outils de synthèse (tableaux, arbres, pourcentages, fréquences).
♦ Construire des outils de représentation (diagrammes et graphiques divers).
♦ Construire des caractères de position d'une série statistique (moyenne, médiane. . .).
Connaissances mathématiques
♦ Calculer des fréquences ou des pourcentages.
♦ Dénombrer.
♦ Calculer une probabilité.
♦ Utiliser la notion de fraction.
Solution possible
Première solution
L'univers est constitué de tous les chemins possibles que la fourmi peut parcourir ne dépassant pas quatre arêtes.
On nomme S l'évènement : « la fourmi survit à cette expérience c'est-à-dire la chaîne de sommets contient exactement un autre A ».
Par exemple :
♦ A − B − C − A est une chaîne pour laquelle la fourmi survit,
♦ A − B − C − D − B est une chaîne pour laquelle la fourmi meurt.
On nomme Ai l'évènement : « la fourmi a parcouru i arête(s)», avec i un entier entre 1 et 4.
P(S) = P(S ∩ A1) + P(S ∩ A2) + P(S ∩ A3) + P(S ∩ A4)
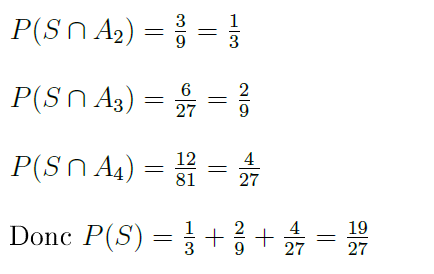
Attention à ne pas se restreindre à un arbre où les branches s'arrêtent dès qu'on obtient le sommet A!
