La course des lutins

Solution

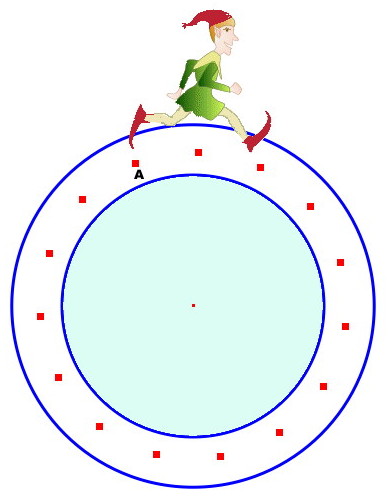Il y a 15 cailloux disposés en cercles, donc 15 intervalles.

En prenant l’intervalle comme unité, Joël fait des sauts de 2, Maël des sauts de 4 et Gaël des sauts de 3.

Gaël va gagner la course en 5 sauts. Pour les deux autres c’est plus difficile : après 7 sauts Joël se trouve sur le caillou juste avant A, et le saut suivant l’amène en B. Il lui faut donc entamer un deuxième tour.

Heureusement, 2 tours correspondent à 30 intervalles, et Joêl se retrouve en A après 15 sauts.

Pour Maël, la course s’avère pénible. 30 n’est pas divisible par 4, il lui faut donc entamer un troisième tour, puis un quatrième ! 60 est divisible par 4, ouf ! Et Maël se retrouve ex-aequo avec Joël.

Compréhension de l’énoncé

L’énoncé est assez long, et des élèves peuvent ne pas comprendre la règle de déplacement des lutins. Il faut bien préciser que chaque lutin choisit une longueur de saut et s’y tient.

De plus le règlement de la course porte sur le nombre de sauts effectués, non sur le temps, dont on ne sait rien.

Il peut être intéressant, une fois ces points éclaircis, de demander aux élèves sur quel lutin ils parient a priori, et d’inscrire les paris au tableau.

Intérêt du problème

Les élèves vont le résoudre de façon très empirique, en faisant effectivement les déplacements. Ils vont vite s’apercevoir de l’intérêt de numéroter les cailloux.

Le résultat devrait surprendre certains (d’où l’intérêt du pari initial). Pour les amener à observer les relations entre les nombres, on peut leur proposer de reprendre la question avec 14, 16, 20 ou 21 cailloux.

Les élèves vont eux-mêmes se poser des questions.

Qui gagne "le plus souvent" ?

Joël et Maël sont-ils toujours ex-aequo ?

Y a -t-il des cas où les trois lutins sont ex-aequo ?

etc

Aux plus avancés, on peut demander de trouver "des règles pour prévoir".