Economie d’énergie : solution
Avec un rectangle (35, 24), fabriquer un rectangle (30,28)
Tout d’abord, est-ce possible ? Il faut pour cela vérifier que 35x24 = 30x28. On peut donc au minimum découper le rectangle en petits carrés unité et les réassembler.
Ce ne serait pas "économique" du tout !
L’idée suivant est de découper en carrés ou rectangles plus grands. En effet : 35x24 = (7x5)x(6x4) = (7x4)X(5x6) = 28x30. On peut tout découper en rectangles 7x4, par exemple. Cela fait quand même 30 morceaux.
Mieux : Le rectangle peut être divisé sur sa longueur en 7 bandes de longueur 5 ; il suffit d’enlever sur la longueur une bande de largeur 5, pour la ramener de 35 à 30.
Le rectangle 5x24 enlevé peut alors être découpé en petits rectangles 5x4 pour faire passer l’autre côté de 24 à 28.
Voilà ce que ça donne :
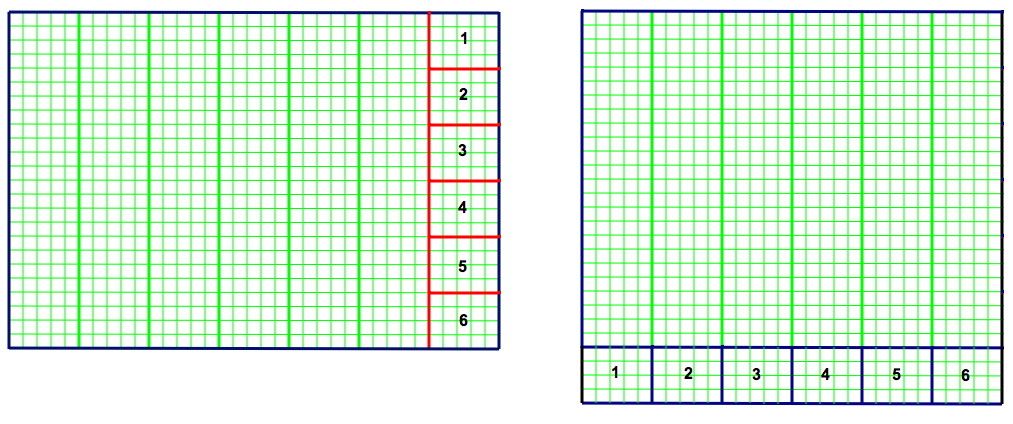 (Cliquer sur l’image pour l’agrandir)
(Cliquer sur l’image pour l’agrandir)
| Bilan : découpage en 7 morceaux, 6 traits de ciseaux, longueur totale de découpe 54 |
Encore mieux : tout aussi facilement, on peut enlever sur la longueur une bande de largeur 7, ce qui la ramène à 28.
Le rectangle 7x24 doit ensuite être redécoupé en petits rectangles 7x 6.
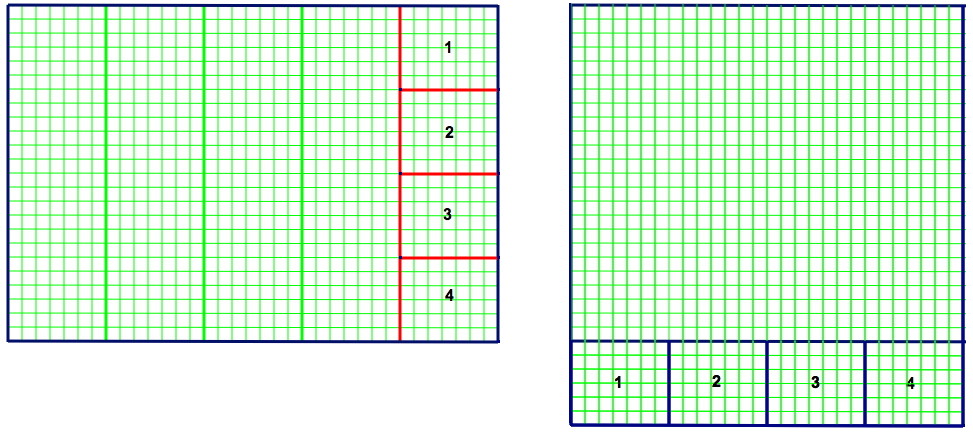
| Bilan : découpage en 5 morceaux, 4 traits de ciseaux, longueur totale de découpe 45 |
Plus les morceaux sont gros, moins il y en a !
Avec des élèves de CM et ou sixième, on peut se contenter de cette solution. Il existe cependant un découpage en deux morceaux, que voici.
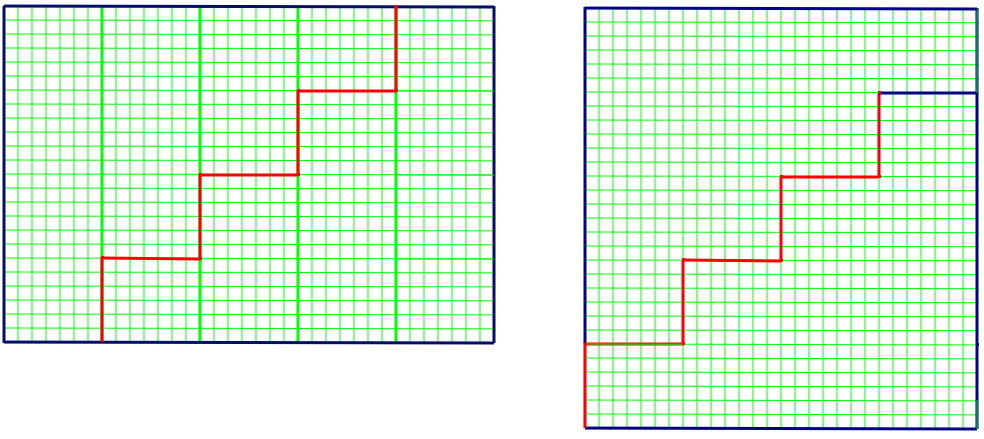
| Bilan : découpage en 2 morceaux, 7 traits de ciseaux, longueur totale de découpe 41 |
Ce découpage est gagnant sur presque toute la ligne. Le découpage effectif sera plus long que le précédent !
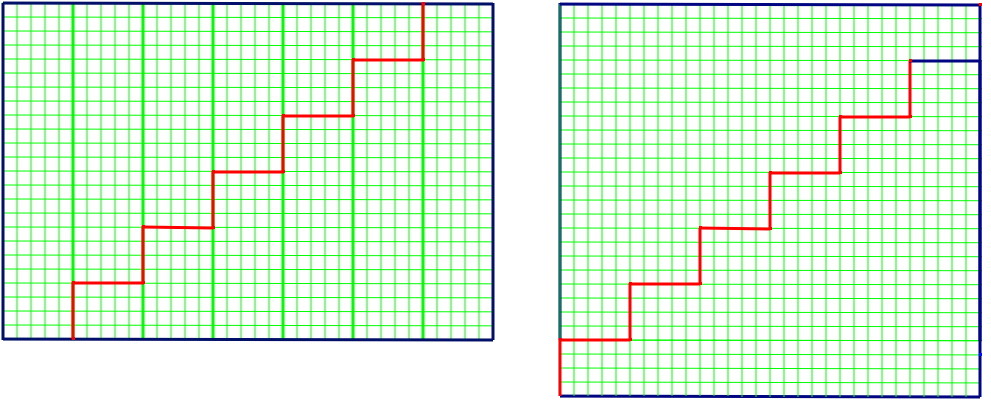
Que donne ce découpage en escalier si l’on reprend la première idée : diminuer la longueur de 5 ?
| Bilan : découpage en 2 morceaux, 11 traits de ciseaux, longueur totale de découpe 49 |
N’en parlons plus.
Ce qui ressort de ces exemples est qu’il vaut mieux diminuer au maximum le plus grand côté, donc transformer la longueur du rectangle initial en largeur du rectangle visé.


Commentaires