D’autres centres : analyse
Cette construction est plus difficile que celle proposée dans "Chercher les centres"(1) et (2).
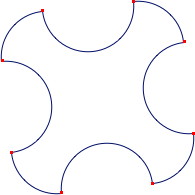
Une erreur fréquente est liée à l’impression, non vérifiée, que les quatre petits arcs appartiennent à un même cercle.
|
|
|
1. Première étape. Les demi-cercles
Certains élèves vont placer leurs centres au jugé, en s’aidant des tracés d’arcs de cercle donnés. Ils peuvent être mécontents du résultat et rester bloqués. Il faut les encourager à chercher la position des centres sur la figure modèle en y ajoutant des tracés.
Ceux qui pensent à inscrire la figure dans un carré peuvent franchir facilement cette étape.
A noter que les éléments donnés permettent de construire un quadrillage :

|

|
Coup de pouce. L’enseignant peut avoir en réserve une figure avec deux demi-cercles tracés, ce qui facilite l’utilisation des symétries de la figure.
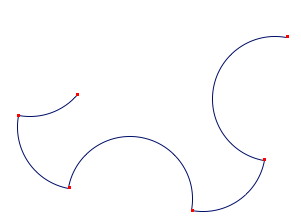 2. Deuxième étape. Les quarts de cercle
2. Deuxième étape. Les quarts de cercle
On a déjà noté que ceux-ci ne sont pas identifiés à vue, mais peuvent être vus comme de petits arcs d’un même cercle dont le centre serait le centre de symétrie de la figure.
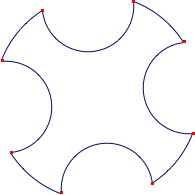
Sur la figure à compléter, deux des petits quarts de cercles sont déjà tracés, mais, comme on peut l’observer ci-dessous, l’erreur restera cependant peu visible, d’autant que la plupart des élèves ne vont pas tracer le cercle entier mais seulement les arcs dont ils auront repéré les extrémités.
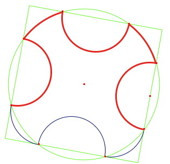
|
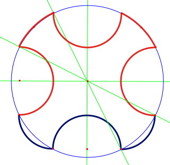
|
Il faut donc prévoir une mise en commun et une discussion sur l’identification précise des centres.
Les élèves qui ont construit un quadrillage ont fait un choix judicieux :
les centres des arcs de cercle sont tous des noeuds du quadrillage.

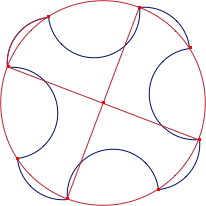
Pour les autres, l’identification des centres des quarts de cercle est moins évidente. Il faut tracer le segment joignant deux centres consécutifs de demi-cercles.
Par exemple sur la figure ci-dessous, un des centres cherchés est le milieu de [IJ], également intersection de[IJ] avec la diagonale du carré.
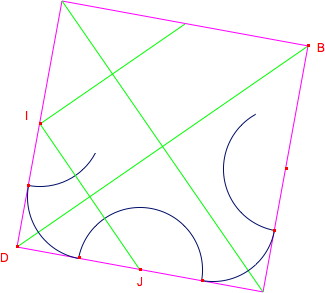


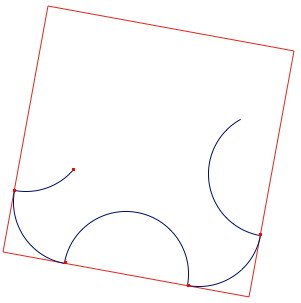
Commentaires