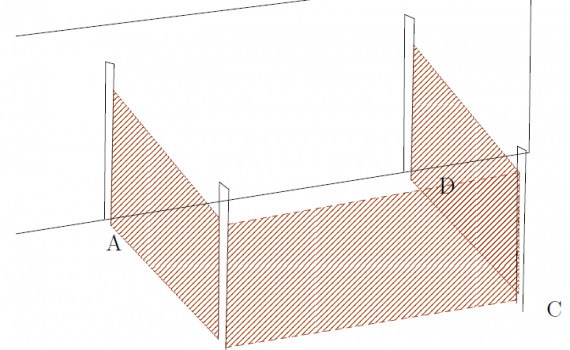
Où faudrait-il placer le point P sur l'hypoténuse de ce triangle BAC pour que le segment [IJ] ait la plus petite longueur possible ?
Situation Problème
Avec un cube de 10 cm d’arête et un sommet A, quels points du cube se trouvent exactement à 15 cm de A ? Comment les déterminer ?
Deux tours de 30 m et 40 m, distantes de 50 m, et un puits entre elles. Comment déterminer sa position si deux oiseaux partent des sommets et arrivent simultanément ?
Avec 21 m de grillage et un mur comme quatrième côté, où placer le point B pour obtenir l’enclos rectangulaire le plus grand ? L’aire varie-t-elle selon sa position ?
Construire des figures aux côtés égaux. Déterminer la longueur des lignes selon la première longueur, puis pour les générations 4, 10, 103, et en général pour la génération n.
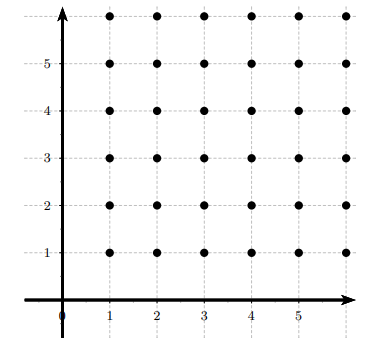
Comment déterminer le nombre de segments différents joignant deux points choisis parmi plusieurs placés sur une feuille ?
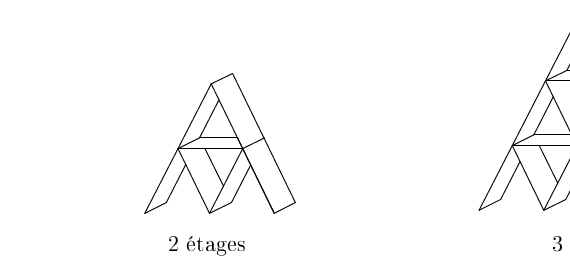
Un château de cartes grandit vite : 2 cartes pour 1 étage, 7 pour 2, 15 pour 3… Combien en faut-il pour 7, 30 ou même 100 étages ?
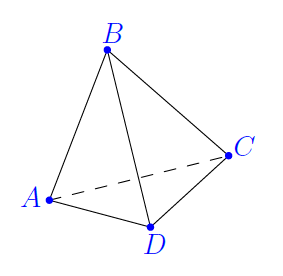
Une fourmi part du point A et se déplace au hasard sur un graphe. Sa survie dépend-elle de revenir à A en quatre arêtes maximum ? Quelle est sa probabilité ?
Quatre jetons dont un « gagnant » vert et trois perdants. Après trois échanges aléatoires dans un sac, quelle est la probabilité de récupérer le jeton gagnant ?
Dans un champ infini de colonnes, quelles trajectoires d’un laser depuis les axes évitent toutes les colonnes ? Comment les décrire et le démontrer ?
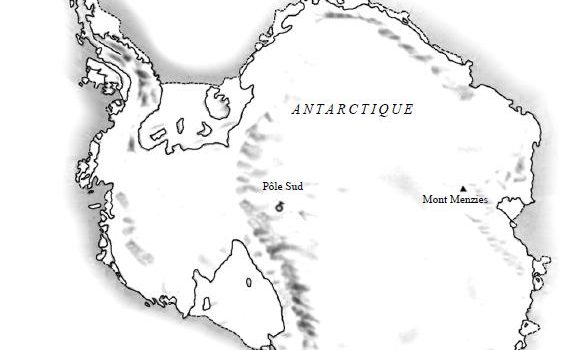
Comment estimer la distance entre le Pôle Sud et le Mont Menzies, et l’aire de l’Antarctique ? Utilisez l’échelle de la carte et expliquez votre méthode.
Comment découper une croix grecque en 2, 3, 4… jusqu’à 100 parties de même aire ? Peut-on trouver une méthode générale pour n’importe quel nombre de parts ?