Mémoire de DEA :

Thèse de Doctorat de Mathématiques :

Soutenue le 19 mars 1992 à l'Université Lyon-I. Composition du jury : J. Brossard (Rapporteur), A. Goldman, J.-F. Le Gall (Rapporteur), E. Pardoux.
Résumé    Thèse

       Dans ce travail nous rassemblons l'essentiel des résultats que nous avons obtenus sur le comportement de l'intégrale du mouvement brownien linéaire, et plus particulièrement sur les différentes distributions associées aux premiers instants de passage des trajectoires par des seuils fixés.

       Ainsi nous avons pu déterminer explicitement la loi conjointe du couple constitué du premier instant de passage du processus «primitive» par un point fixé et de la position occupée par le mouvement brownien à cet instant. On retrouve en particulier les lois marginales de ce couple découvertes par M. Goldman (1971) et Ju. P. Gor'kov (1975), ainsi que la loi du premier instant de retour à l'origine obtenue par H.P. McKean (1963). Ce résultat nous a permis de débloquer plusieurs problèmes ouverts. Nous obtenons ainsi les distributions de plusieurs fonctionnelles associées à l'intégrale du mouvement brownien : temps de passage successifs, dernier instant de passage, temps de séjour, excursions...

       Nous étudions ensuite la position de la primitive du mouvement brownien lorsque ce dernier atteint une barrière simple ou bilatère. Ce type de fonctionnelle apparaît naturellement dans certains problèmes d'optimisation étudiés par M. Lefèbvre (1989). une nouvelle approche nous a permis de retrouver et d'améliorer ses résultats.

       Nous explicitons finalement la distribution de certaines fonctionnelles relatives à l'intégrale du mouvement brownien lorsque cette dernière est soumise à une dérive parabolique ou cubique. On retrouve en particulier un résultat de P. Groeneboom (1989) concernant le mouvement brownien avec dérive parabolique.

       Une description de quelques problèmes restant encore ouverts termine ce travail.

Table des matières Introduction Chapitre I : Équation de Langevin Introduction Description de l'expérience physique Une solution de l'équation de Langevin : un processus gaussien stationnaire \((x_t)_{t\geqslant 0}\) Le nombre de zéros de \((x_t)_{t\geqslant 0}\) Chapitre II : Étude d'un cas particulier : l'intégrale du mouvement brownien Introduction La loi conjointe du couple \((\tau_a,B_{\tau_a})\) sous la probabilité \(\mathbb{P}_{(a,y)}\) Les lois des variables aléatoires \(\tau_a\) et \(B_{\tau_a}\) sous la probabilité \(\mathbb{P}_{(a,y)}\) La loi conjointe du couple \((\tau_a,B_{\tau_a})\) sous la probabilité \(\mathbb{P}_{(x,y)}\) Sur l'intégrale du mouvement brownien Sur le premier instant de passage de l'intégrale du mouvement brownien Sur les temps de passages successifs de l'intégrale du mouvement brownien Dernier instant de passage pour l'intégrale du mouvement brownien Sur les excursions de l'intégrale du mouvement brownien Les excursions de l'intégrale du mouvement brownien Les moments du temps de séjour de l'intégrale du mouvement brownien Les lois conjointes des couples \((\sigma_b,X_{\sigma_b})\) et \((\sigma_{ab},X_{\sigma_{ab}})\) sous la probabilité \(\mathbb{P}_{(x,y)}\) Un problème d'optimisation Extensions diverses À propos de l'intégrale du mouvement brownien Sur la distribution de certaines fonctionnelles de l'intégrale du mouvement brownien avec dérives parabolique ou cubique Chapitre III : Problèmes ouverts Premier instant d'atteinte d'une barrière bilatère \(\{a,b\}\) pour le processus \((X_t)_{t\geqslant 0}\) Premier instant de sortie d'un quadrant pour le processus \((X_t,B_t)_{t\geqslant 0}\) Temps de séjour du processus \((X_t)_{t\geqslant 0}\) Primitives itérées du mouvement brownien L'opérateur différentiel \(d^4/dx^4\)

Publications issues de la thèse (par ordre d'apparition) :

• Comptes Rendus de l'Académie des Sciences, t. 311 (1990), 461-464.
• Annales de l'Institut Henri Poincaré Section B 27(3) (1991), 385-405.
• Comptes Rendus de l'Académie des Sciences, t. 321 (1995), 903-908.
• Stochastic Processes and their Applications 49 (1994), 57-64.
• Comptes Rendus de l'Académie des Sciences, t. 314 (1992), 1053-1056.
• Journal of Applied Probability 30 (1993), 17-27.
• Communications on Pure and Applied Mathematics XLIX (1996), 1299-1338.

Eugène Boudin (1824-1898) – Rivage de Portrieux, 1874

Masquer le résumé

Thèse d'habilitation à diriger des recherches :

Soutenue le 3 juillet 1995 à l'Université Lyon-I. Composition du jury : J. Brossard, A. Goldman, J.-P. Imhof, J.-F. Le Gall, P. McGill (Rapporteur), E. Pardoux, B. Roynette (Rapporteur), M. Yor (Rapporteur).
Résumé    Thèse

       L'ensemble de nos travaux est essentiellement consacré à l'étude de la primitive du mouvement brownien; plus particulièrement il est orienté vers la détermination explicite des distributions de probabilité de diverses fonctionnelles associées à ce processus. Les motivations et le contexte historique de cette étude, qui débute principalement avec les travaux de P. Langevin, H.P. McKean et M. Kac sont décrits en détail dans le chapitre d'introduction de notre thèse de Doctorat.

       Le point de départ de notre étude fut la détermination explicite de la loi du premier instant de passage \(\tau_a\) de l'intégrale du mouvement brownien \((X_t)_{t\ge0}\) par un seuil fixé \(a\), couplé avec la position du mouvement brownien \((B_t)_{t\ge0}\) à cet instant, lorsque le processus markovien bidimensionnel \((X_t,B_t)_{t\ge0}\) démarre d'un point quelconque \((x,y)\in\mathbb{R}^2\). Ce résultat qui résolvait un problème ouvert posé dans l'article A winding problem for a resonator driven by a white noise, datant de 1963, de H.P. McKean a permis de débloquer de nombreuses questions et a joué un rôle déterminant dans la suite de notre recherche.

       Pour citer un exemple significatif, la connaissance de la distribution conjointe du couple \((\tau_a,B_{\tau_a})\) nous a conduit à celle du dernier temps \(\tau_{a,T}^-\) d'atteinte du point \(a\) par le processus \((X_t)_{t\ge0}\), avant un instant fixé \(T\). Dès lors, l'écriture explicite de cette dernière loi permet d'en décrire le comportement asymptotique lorsque \(T\) tend vers zéro. Cette estimation a été, en particulier, exploitée par S. Aspandiiarov et J.-F. Le Gall au cours d'un travail en liaison avec l'étude de l'équation de Burgers.

       Par ailleurs, nous avons engagé une étude approfondie de diverses excursions du processus \((X_t,B_t)_{t\ge0}\), ayant toujours pour objectif la détermination exacte et explicite de la loi de certaines fonctionnelles. En faisant appel à la théorie générale des excursions d'un processus de Markov, nous avons pu exhiber par exemple la loi du quadruplet \((\tau_{a,T}^-,B_{\tau_{a,T}^-},\tau_{a,T}^+,B_{\tau_{a,T}^+})\) constitué des dernier et premier temps de passage par le seuil \(a\) respectivement postérieur et antérieur à l'instant déterministe \(T\), et des positions relatives du mouvement brownien. Nous en avions auparavant obtenu par une technique markovienne seulement quelques lois marginales. Une recherche portant sur l'aire d'une boucle d'excursion associée au processus \((X_t,B_t)_{t\ge0}\) nous a ensuite confrontés à la primitive du processus d'Ornstein-Uhlenbeck, dont nous avons également explicité quelques distributions afférentes.

       Plus généralement, les excursions de l'intégrale du mouvement brownien hors d'un point \(a\) (sans restriction temporelle à présent) font apparaître la suite des temps de visite successifs \((\mathbf{t}_n)_{n\ge 1}\) du point \(a\) par le processus \((X_t)_{t\ge0}\). Cette suite présente un comportement très différent de celui qui caractérise les excursions browniennes, cas pour lequel une telle suite ne peut être définie en vertu de l'irrégularité des trajectoires browniennes. En faisant appel à la transformation de Kontorovich-Lebedev nous avons pu obtenir pour la loi conjointe du couple \((\mathbf{t}_n,B_{\mathbf{t}_n})_{n\ge 1}\) une formule simple ne requérant pas l'usage des intégrales multiples.

       Divers problèmes demeurent actuellement non résolus. Notamment: la loi de probabilité du premier instant de sortie d'un intervalle borné \([a,b]\) de \(\mathbb{R}\) par la primitive du mouvement brownien reste inconnue; la distribution du temps séjourné dans \([a,b]\) par \((X_t)_{t\ge0}\) n'est toujours pas explicitée.

       D'autres questions, de nature géométrique, se posent également : les trajectoires du processus bidimensionnel \((X_t,B_t)_{t\ge0}\) comportent-elles des points multiples ? est-il possible de caractériser les ensembles polaires pour ce processus ? Quelle est l'exacte mesure de Hausdorff de la courbe \(t\mapsto(X_t,B_t)\) ?

Table des matières Introduction Sur l'intégrale du mouvement brownien Comptes Rendus de l'Académie des Sciences, t. 311 (1990), 461-464. Sur le premier instant de passage de l'intégrale du mouvement brownien Annales de l'Institut Henri Poincaré Section B 27(3) (1991), 385-405. L'intégrale du mouvement brownien Journal of Applied Probability 30 (1993), 17-27. Dernier instant de passage pour l'intégrale du mouvement brownien Stochastic Processes and their Applications 49 (1994), 57-64. Sur les excursions de l'intégrale du mouvement brownien Comptes Rendus de l'Académie des Sciences, t. 314 (1992), 1053-1056. Quelques applications de la théorie des excursions à l'intégrale du mouvement brownien Séminaire de Probabilités XXXVIII, Lecture Notes in Mathematics 1801 (2003), 109-195. Sur les temps de passages successifs de l'intégrale du mouvement brownien Comptes Rendus de l'Académie des Sciences, t. 321 (1995), 903-908. Les temps de passages successifs de l'intégrale du mouvement brownien Annales de l'Institut Henri Poincaré Section B 33(1) (1997), 1-36. Some martingales related to the integral of Brownian motion. Application to passage times and transience Stochastics and Stochastics Reports 58 (1996), 285-302. Sur la distribution de certaines fonctionnelles de l'intégrale du mouvement brownien avec dérives parabolique ou cubique Communications on Pure and Applied Mathematics XLIX (1996), 1299-1338. Quelques martingales associées à l'intégrale du processus d'Ornstein-Uhlenbeck. Application à l'étude des premiers instants de passage Journal of Theoretical Probability 11(1) (1998), 127-156. Annexe: récapitulatif Bibliographie

Claude Monet (1840-1926) – Débâcle sur la Seine : les glaçons, 1880

Masquer le résumé

Sur le premier instant de passage de l'intégrale du mouvement brownien
Annales de l'I. H. P. Sect. B 27(3) (1991), 385-405.
Référence MathSciNet : MR1131839 (92m:60073)
Résumé    Article

       This paper concerns a famous problem of Kac, Rice and Potter on the windings of Brownian motion in the phase plane. One looks to compute explicitly the joint law of the hitting time and hitting distribution for the process \((x+ty+ \int_0^t B_s\,ds, B_t+y\)) on vertical lines \(\{a\}\times \mathbb{R}.\) The problem can be reduced to solving a PDE with boundary conditions, which is solved here by taking a Kantorovich-Lebedev transform; McKean looked at this in the case \(x=a\). The analogue for (one or two) horizontal lines is easier; joint laws can be computed by using the Feynman-Kac formula.

Pierre-Auguste Renoir (1841-1919) – Le Déjeuner des canotiers, 1880-1881

Masquer le résumé

L'intégrale du mouvement brownien
Journal of Applied Probability 30 (1993), 17-27.
Référence MathSciNet : MR1206349 (94a:60120)   DOI:10.2307/3214618
Résumé   Article

       Let \((B_t)_{t\ge 0}\) denote the Brownian motion process starting at the origin, let \(X_t=\int^t_0B_sds\) be its primitive and let \(U_t=(X_t+x+ty,B_t+y)\), \(t\ge0\), be the associated bidimensional process starting from a point \((x,y)\in \mathbb{R}^2\). In this paper we present an elementary procedure for rederiving the formula of M. Lefebvre [SIAM J. Appl. Math. 49 (1989), no. 5, 1514-1523] giving the Laplace-Fourier transform of the distribution of the pair \((\sigma_a,U_{\sigma_a})\), as well as Lachal's formulae (1991) giving the explicit Laplace-Fourier transform of the law of the couple \((\sigma_{ab},U_{\sigma_{ab}})\), where \(\sigma_a\) and \(\sigma_{ab}\) denote, respectively, the first hitting time of \(\mathbb{R}\times \{a\}\) from the right and the first hitting time of the double-sided barrier \(\mathbb{R}\times \{a,b\}\) by the process \((U_t)_{t\ge 0}\). This method, which unifies and considerably simplifies the proofs of these results, is in fact a `vectorial' extension of the classical technique of D. A. Darling and A. J. F. Siegert [Ann. Math. Statist. 24 (1953), 624-639]. It rests on an essential observation [A. Lachal, «Étude des trajectoires de la primitive du mouvement brownien», Thèse de Doctorat, 1992; per bibl.] of the Markovian character of the bidimensional process \((U_t)_{t\ge 0}\). Using the same procedure, we subsequently determine the Laplace-Fourier transform of the conjoint law of the quadruplet \((\sigma_a,U_{\sigma_a},\sigma_b,U_{\sigma_b})\).

Edouard Manet (1832-1883) – Monet dans son bateau atelier, 1874

Masquer le résumé

Dernier instant de passage pour l'intégrale du mouvement brownien
Stochastic Processes and their Applications 49 (1994), 57-64.
Référence MathSciNet : MR1258281 (95a:60109)   DOI:10.1016/0304-4149(94)90111-2
Résumé    Article

       Let \((B_t)_{t\ge 0}\) be the standard Brownian motion. Fix \(T > 0\) and look at the excursion of the process \(X_t=x+\int_0^t B_s\,ds\), \(t\ge0\), from \(a\) which straddles \(T\). The paper shows how to compute the joint law of the excursion interval and the terminal value of \(B\). In fact, since the semigroup of \(((X_t, B_t))_{t\ge 0}\) is known from the work of McKean, the problem reduces to calculating the law of \((B_t)_{t\ge 0}\) when \((X_t)_{t\ge0}\) hits \(a\). But this the author already knows. The answers are explicit and yield a simple form for the law of the excursion interval spanning \(T\) in terms of the Bessel function \(K_0\).

Alfred Sisley (1839-1899) – Inondation à Port Marly, 1876

Masquer le résumé

Sur la distribution de certaines fonctionnelles de l'intégrale du mouvement brownien avec dérives parabolique et cubique
Communications on Pure and Applied Mathematics XLIX (1996), 1299-1338.
Référence MathSciNet : MR1414588 (97j:60150)   DOI:10.1002/(SICI)1097-0312(199612)49:12<1299::AID-CPA4>3.0.CO;2-5
Résumé

       Soit \((B_t)_{t\geq 0}\) le mouvement brownien linéaire démarrant de l'origine, \(X_t = \int_0^t B_u \, du\). On considère le processus \(U^{z,w}_t = (X_t + \frac{1}{2} t^2 z + \frac{1}{6} t^3 w, B_t + tz + \frac{1}{2} t^2 w), t \geq s\) (\(s>0\) fixé), constitué du mouvement brownien auquel se superpose une dérive parabolique \(tz + \frac{1}{2} t^2 w\), et de sa primitive soumise à la dérive cubique correspondante \(\frac{1}{2} t^2 z + \frac{1}{6} t^3 w\). Dans cet article nous déterminons les distributions de diverses fonctionnelles (premiers instants d'atteinte, derniers instants de sortie, maxima) associées au processus \((U^{z,w}_t)_{t \geq s}\).

Vincent Van Gogh (1853-1890) – L'Église d'Auvers-sur-Oise, 1890

Masquer le résumé

Quelques martingales associées à l'intégrale du processus d'Ornstein-Uhlenbeck. Application à l'étude des premiers instants d'atteinte
Stochastics and Stochastics Reports 58 (1996), 285-302.
Référence MathSciNet : MR1424696 (98e:60059)   DOI:10.1080/17442509608834078
Résumé

       Soit \((O_t)_{t \geq 0}\) le processus d'Ornstein-Uhlenbeck de paramètre \(\beta\), démarrant de \(y\) et \(X_t =\int_0^ t O_s \,ds + x\). Dans cet article, après avoir construit diverses martingales associées au processus bidimensionnel \((X_t,O_t)_{t \geq 0}\) , nous explicitons les transformées de Laplace-Fourier des couples \((\sigma_a, X_{\sigma_a}), (\sigma_{ab},X_{\sigma_{ab}} )\) et du quadruplet \((\sigma_a, X_{\sigma_a},\sigma_b, X_{\sigma_b})\) où \(\sigma_a=\inf\{t > 0 \colon O_t= a\}\) et \(\sigma_{ab}= \inf \{t > 0 \colon O_t\in \{a,b\}\}\). Nous étendons ensuite les résultats obtenus au cas d'un processus d'Ornstein-Uhlenbeck soumis à une dérive «hyperbolique» de la forme \(z {\sinh \beta t \over\beta} + w{\cosh \beta t-1\over\beta^ 2}\).

Joseph Mallord William Turner (1775-1851) – Pluie, vapeur et vitesse - Le grand chemin de fer de l'Ouest, 1844

Masquer le résumé

Les temps de passages successifs de l'intégrale du mouvement brownien
Annales de l'I. H. P. Sect. B 33(1) (1997), 1-36.
Référence MathSciNet : MR1440254 (98g:60148)   DOI:10.1016/S0246-0203(97)80114-8
Résumé    Article

       Soit \((B_t)_{t \geq 0}\) un mouvement brownien linéaire et \(X_t=x +\int_0^ t B_s \,ds\). Dans ce travail nous explicitons la distribution de plusieurs fonctionnelles du processus bidimensionnel \((X_t, B_t)_{t \geq 0}\) intimement liées au premier instant de passage de celui-ci.

Jean-Baptiste Olive (1848-1936) – Le vieux port - Marseille

Masquer le résumé

Regular points for the successive primitives of Brownian motion
Journal of Mathematics of Kyoto University 37(1) (1997), 99-119.
Référence MathSciNet : MR1447364 (98g:60149)   DOI:10.1215/kjm/1250518399
Résumé    Article

       Let \((B(t))_{t\geq 0}\) be the linear Brownian motion starting at \(0\), and set \(X_n(t) = {1\over n!}\int_0^ t (t-s)^ n\, dB(s)\). In this paper we write out a Wiener's test about regular points for the \((n+1)\)-dimensional process \((B,X_1,\ldots ,X_n)\), and we next apply this test to two examples of thornshaped sets.

Pierre-Auguste Renoir (1841-1919) – Bal du moulin de la Galette, 1876

Masquer le résumé

Local asymptotic classes for the successive primitives of Brownian motion
Annals of Probability 25(4) (1997), 1712-1734.
Référence MathSciNet : MR1487433 (98j:60112)   DOI:10.1214/aop/1023481108
Résumé    Article

       Let \((B(t))_{t\geq 0}\) be the linear Brownian motion starting at \(0\), and set \(X_n(t) ={1\over n!}\int_0^ t (t-s)^ n\, dB(s)\). H. Watanabe [Trans. Amer. Math. Soc., 148 (1970), pp. 233-248] stated a law of the iterated logarithm for the process \((X_1(t))_{t\geq 0}\) among other things. In this paper is proposed an elementary proof of this fact, which can be extended to the general case \(n\geq 1\). Next, we study the local asymptotic classes (upper and lower) of the \((n+1)\)-dimensional process \(U_n=(B,X_1,\ldots ,X_n)\) near zero and infinity, and the obtained results are extended to the case where \(B\) is the \(d\)-dimensional Brownian motion.

Berthe Morisot (1841-1895) – Port de Lorient, 1869

Masquer le résumé

Some martingales related to the integral of Brownian motion. Application to the passage times and transience
Journal of Theoretical Probability 11(1) (1998), 127-156.
Référence MathSciNet : MR1607384 (99f:60146)   DOI:10.1023/A:1021646925303
Résumé

       Let \((B_t)_{t\geq 0}\) be the standard linear Brownian motion started at \(y\) and set \(X_t=x+\int_0^ t B_s\,ds\), \(U_t=(X_t,B_t)\). In this paper we introduce some martingales related to the Markov process \((U_t)_{t\geq 0}\), which allow us to calculate explicitly the probability laws of several passage times associated to \(U\) in a probabilistic way. With the aid of an appropriate supermartingale, we also establish the transience of the process \((U_t)_{t\geq 0}\).

Balthasar van der Ast (1593-1657) – Nature morte aux fruits, 1620

Masquer le résumé

First exit time from a bounded interval for a certain class of additive functionals of Brownian motion
Journal of Theoretical Probability 13(3) (2000), 733-775.
Référence MathSciNet : MR1785528 (2001i:60126)   DOI:10.1023/A:1007810528683
Résumé

       Let \((B_t)_{t\ge 0}\) be standard Brownian motion starting at \(y\), \(X_t = x+\int_0^t V(B_s) \, ds\), \(x\in (a,b)\), with \(V(y)= y^{\gamma}\) if \(y\ge 0\), \(V(y)= -K(-y)^{\gamma}\) if \(y\le 0\), where \(\gamma >0\) and \(K\) is a given positive constant. Set \(\tau_{ab} = \inf \{ t>0 : X_t \notin (a,b) \}\) and \(\sigma_0 = \inf\{ t>0 : B_t = 0\}\).

       In this paper we give several informations about the random variable \(\tau_{ab}\). We namely evaluate the moments of the random variables \(B_{\tau_{ab}}\) and \(B_{\tau_{ab}\wedge \sigma_0}\), and also show how to calculate the expectations \(\mathbb{E} (\tau_{ab}^m B_{\tau_{ab}}^n)\) and \(\mathbb{E} ((\tau_{ab}\wedge\sigma_0)^m B_{\tau_{ab}\wedge\sigma_0}^n)\). Then, we explicitly determine the probability laws of the random variables \(B_{\tau_{ab}}\) and \(B_{\tau_{ab}\wedge \sigma_0}\) as well as the probability \(\mathbb{P}\{ X_{\tau_{ab}}=a \mbox{ (or \(b\))}\}\) by means of special functions.

Johan Barthold Jongkind (1819-1891) – Le bassin du port : entrepôt de Bruxelles, 1874

Masquer le résumé

Study of some new integrated statistics: computation of Bahadur efficiency, relation with non-standard boundary value problems
Mathematical Methods of Statistics 10(1) (2001), 73-104.
Référence MathSciNet : MR1841809 (2002j:62066)
Résumé

       Let \(p\) be a positive integer. This paper deals with \(p\)-fold integrated empirical process the limiting process of which being the \(p\)-fold integrated Brownian bridge, together with some related Kolmogorov-Smirnov, Cramér-von Mises and Watson-type statistics. The Bahadur theory is applied to those statistics in case of shift alternatives and comparisons with classical non-integrated case (\(p=0\)) are made. Several boundary value problems arise in this study and are stated on the one hand in the context of relationships between covariance and Green functions, and on the other hand in the context of optimality for the Bahadur-Raghavachari inequality. The results that are displayed here extend certain of Henze and Nikitin [1,2] who considered the case \(p=1\) and others of the author.

[1] Henze, N. and Nikitin, Ya. Yu. A new approach to goodness-of-fit tests based on the integrated empirical process, J. Nonpar. Statist. 12 (2000), 391-416.

[2] Henze, N. and Nikitin, Ya. Yu. Watson-type goodness-of-fit tests based on the integrated empirical process, preprint of University of Karlsruhe, 1999.

Paul Cézanne (1839-1906) – Nature morte - Compotier, 1879-1882

Masquer le résumé

Bridges of certain Wiener integrals. Prediction properties, relation with polynomial interpolation and differential equations. Application to goodness-of-fit testing
in Bolyai Society Mathematical Studies X. Limit Theorems, Balatonlelle (Hungary), 1999. Budapest, 2002, 1-51.
Référence MathSciNet : MR1979998 (2004e:60140)
Résumé

       Let \((W(t))_{t\ge 0}\) and \((\beta(t))_{t\ge 0}\) be respectively standard Wiener process started at 0 and standard Brownian bridge, and denote by \(W_n(t)=\frac{1}{n!} \int_0^t (t-s)^n\, dW(s)\) and \(\beta_n(t)=\frac{1}{n!} \int_0^t (t-s)^n\, d\beta(s)\) their \(n\)-fold primitives. This paper deals with the conditioned process \(B_n = (W_n(t)| W_0(1)=\ldots = W_n(1)=0)_{0\le t\le 1}\) which shall be called `bridge' associated with \(W_n\). Many properties are drawn for this process. We give several representations by means of time-inversion, random drift and conditioning \(\beta_n\). The prediction problem for \(B_n\) is solved, involving some interpolation poynomials; this may provide a probabilistic interpretation for those poynomials. We also found a connexion between the covariance functions for \(B_n\) and \(\beta_n\) and the Green functions for various boundary value problems on the interval [0,1] related to the differential operator \(d^{2n+2}/dx^{2n+2}\). On the other hand, some formulas are derived for the probability distributions of the maximum for the random variables \(B_n\), \(|B_n|\), \(\beta_n\), \(|\beta_n|\). Next we propose some statistics of the type of empirical distributions whose limiting processes are \(B_n\) and \(\beta_n\). Finally, we elaborate several Kolmogorov-Smirnov-like tests of goodness-of-fit.

Paul Cézanne (1839-1906) – Jas de Bouffan, le bassin, 1876

Masquer le résumé

Some probability distributions in modeling DNA replication
Annals of Applied Probability 13(3) (2003), 1207-1230.
Référence MathSciNet : MR1994049 (2004k:60239)   DOI:10.1214/aoap/1060202839
Résumé    Article

       By using some quasi-renewal equations and functional differential equations, we explicitly compute the Laplace transforms of some random variables introduced by Cowan and Chiu in modeling the mechanism of replication of a DNA molecule, [1] and [2]. These Laplace transforms are expressed by means of infinite product arising in the theory of partitions.

[1] R. Cowan. Stochastic models for DNA replication, in The Handbook of Statistics, Vol. 20, eds. C.R. Rao and D.N. Shanbhag, Elsevier, 2001.

[2] R. Cowan and S.N. Chiu. Stochastic model of fragment formation when DNA replicates, Journal of Applied Probability 31 (1994), 301-308.

Vincent Van Gogh (1853-1890) – Champ de blé avec cyprès, 1889

Masquer le résumé

Applications de la théorie des excursions à l'intégrale du mouvement brownien
Séminaire de Probabilités XXXVIII, Lecture Notes in Mathematics 1801 (2003), 109-195.
Référence MathSciNet : MR2053045 (2005g:60128)   DOI:10.1007/b94376
Résumé

       Soit \((B_t)_{t\ge 0}\) le mouvement brownien linéaire démarrant de \(y\) et posons \(X_t=x+\int_0^t B_s ds\) et \(U_t=(X_t, B_t)\). Introduisons les différents temps de passage enjambant un instant fixé \(T>0\) suivants :

• \(\tau_{a,T}^- = \sup\{t\le T: X_t=a\}\),
• \(\tau_{a,T}^+ = \inf\{t\ge T: X_t=a\}\),
• \(\sigma_{b,T}^- = \sup\{t\le T: B_t=b\}\),
• \(\sigma_{b,T}^+ = \inf\{t\ge T: B_t=b\}\),
• \(\sigma_{ab,T}^- = \sup\{t\le T: B_t\in\{a,b\}\}\),
• \(\sigma_{ab,T}^+ = \inf\{t\ge T: B_t\in\{a,b\}\}\).

Dans ce travail constitué de trois parties, nous explicitons, en faisant appel à la théorie générale des excursions, les lois des divers processus d'excursion enjambant \(T\) associés à \((U_t)_{t\ge 0}\) et aux temps de passage précédents, puis en déduisons les distributions des vecteurs aléatoires

• \((\tau_{a,T}^-,B_{\tau_{a,T}^-},\tau_{a,T}^+,B_{\tau_{a,T}^+})\),
• \((\sigma_{b,T}^-,X_{\sigma_{b,T}^-},\sigma_{b,T}^+,X_{\sigma_{b,T}^+})\),
• \((\sigma_{ab,T}^-,X_{\sigma_{ab,T}^-},\sigma_{ab,T}^+,X_{\sigma_{ab,T}^+})\),

ainsi que celles d'autres fonctionnelles s'y rapportant.

Johan Barthold Jongkind (1819-1891) – L'église de Overschie, 1866

Masquer le résumé

Distributions of sojourn time, maximum and minimum for pseudo-processes governed by higher-order heat-type equations
Electronic Journal of Probability 8 (2003), paper no. 20, 1-53.
Référence MathSciNet : MR2041821 (2005j:60082)   DOI:10.1214/EJP.v8-178
Résumé    Article

       The higher-order heat-type equation \(\partial u/\partial t=\pm\partial^{n} u/ \partial x^{n}\) has been investigated by many authors. With this equation is associated a pseudo-process \((X_t)_{t\ge 0}\) which is governed by a signed measure. In the even-order case, Krylov, [2], proved that the classical arc-sine law of Paul Lévy for standard Brownian motion holds for the pseudo-process \((X_t)_{t\ge 0}\), that is, if \(T_t\) is the sojourn time of \((X_t)_{t\ge 0}\) in the half line \((0,+\infty)\), then \(\mathbb{P}(T_t\in\,ds)=\frac{ds}{\pi\sqrt{s(t-s)}}\). Orsingher, [4], and next Hochberg and Orsingher, [1], obtained a counterpart to that law in the odd cases \(n=3,5,7.\) Actually Hochberg and Orsingher, [1], proposed a more or less explicit expression for that new law in the odd-order general case and conjectured a quite simple formula for it. The distribution of \(T_t\) subject to some conditioning has also been studied by Nikitin and Orsingher, [3], in the cases \(n=3,4.\) In this paper, we prove that the conjecture of Hochberg and Orsingher, [1], is true and we extend the results of Nikitin and Orsingher for any integer \(n\). We also investigate the distributions of maximal and minimal functionals of \((X_t)_{t\ge 0}\).

[1] Hochberg, K.J. and Orsingher, E. The arc-sine law and its analogs for processes governed by signed and complex measures. Stochastic Process. Appl. 52 (1994), no. 2, 273-292.

[2] Krylov, V. Yu. Some properties of the distribution corresponding to the equation \(\frac{\partial u}{\partial t}=(-1)^{q+1} \frac{\partial^{2q} u}{\partial^{2q} x}\). Soviet Math. Dokl. 1 (1960), 760-763.

[3] Nikitin, Ya. Yu. and Orsingher, E. On sojourn distributions of processes related to some higher-order heat-type equations. J. Theoret. Probab. 13 (2000), no.4, 997-1012.

[4] Orsingher, E. Processes governed by signed measures connected with third-order `heat-type' equations. Lithuanian Math. J. 31 (1991), no. 2, 220-231.

Alfred Sisley (1839-1899) – L'automne : bords de la Seine près de Bougival, 1873

Masquer le résumé

Probabilistic approach to Page's formula for the entropy of a quantum subsystem
Stochastics 78(3) (2006), 157-178.
Référence MathSciNet : MR2241914 (2007j:81020)   DOI:10.1080/17442500600737133
Résumé

       Page conjectured [Phys. Rev. Lett. 71, 1291-1294 (1993)] that if a quantum system of Hilbert space dimension \(mn\) is in a random pure state, the average entropy of a subsystem of dimension \(m\le n\) should be given by the simple and elegant formula \(S_{m,n}=\sum_{k=n+1}^{mn}\frac 1k-\frac{m-1}{2n}\). This formula appeared to be true and was first proved by Foong and Kanno [Phys. Rev. Lett. 72, 1148-1151 (1994)] by using Fourier transform, and next by Sánchez-Ruiz [Phys. Rev. E 52, 5653-5655 (1995)] and by Sen [Phys. Rev. Lett. 77, 1-3 (1996)] by using random matrix theory connected with generalized Laguerre polynomials.

       Adopting this last viewpoint, we detail the probabilistic approach to this problem. Especially, viewing any Gaussian vector as a product of a uniformly distributed unitary vector by an Erlang distribution, we give a new insight for the different entropies introduced by Page.

Claude Monet (1840-1926) – Le Pont d'Argenteuil, 1874

Masquer le résumé

Some explicit ditributions related to the first exit time from a bounded interval for certain functionals of Brownian motion
Journal of Theoretical Probability 19(4) (2006), 757-771.
Référence MathSciNet : MR2279602   DOI:10.1007/s10959-006-0039-9
Résumé

       Let \((B_t)_{t\ge 0}\) be standard Brownian motion starting at \(y\) and set \(X_t=x+\int_0^t V(B_s) \, ds\) for \(x\in (a,b)\), with \(V(y)= y^{\gamma}\) if \(y\ge 0\), \(V(y)= -K(-y)^{\gamma}\) if \(y\le 0\), where \(\gamma\) and \(K\) are some given positive constants. Set \(\tau_{ab} = \inf \{t>0:X_t \notin (a,b)\}\). In this paper we provide some formulas for the probability distribution of the random variable \(B_{\tau_{ab}}\) as well as for the probability \(\mathbb{P}\{X_{\tau_{ab}}=a\) (or \(b)\}\). The formulas corresponding to the particular cases \(x=a\) or \(b\) are explicitly expressed by means of hypergeometric functions.

Claude Monet (1840-1926) – Impression, soleil levant, 1872

Masquer le résumé

Minimal cyclic random motion in \(\mathbb{R}^n\) and hyper-Bessel functions (avec E. Orsingher et S. Leorato, Università di Roma “La Sapienza”)
Annales de l'I. H. P. Sect. B 42(6) (2006), 753-772.
Référence MathSciNet : MR2269237   DOI:10.1016/j.anihpb.2005.11.002
Résumé    Article

       We obtain the explicit distribution of the position of a particle performing a cyclic, minimal, random motion with constant velocity \(c\) in \(\mathbb{R}^n\). The \(n+1\) possible directions of motion as well as the support of the distribution form a regular hyperpolyhedron (the first one having constant sides and the other expanding with time \(t\)), the geometrical features of which are here investigated.

       The distribution is obtained by using order statistics and is expressed in terms of hyper-Bessel functions of order \(n+1\). These distributions are proved to be connected with \((n+1)\)th order p.d.e. which can be reduced to Bessel equations of higher order.

       Some properties of the distributions obtained are examined. This research has been inspired by a conjecture formulated in Orsingher and Sommella [1] which is here proved to be false.

[1] E. Orsingher and A.M. Sommella (2004). A cyclic random motion in \(R^3\) with four directions and finite velocity, Stoch. Stoch. Rep, 76(2), 113-133.

John Singer Sargent (1856-1925) – Place Navona, Rome, 1907

Masquer le résumé

Cyclic random motions in space \(\mathbb{R}^d\) with \(n\) directions
ESAIM: Probability and Statistics 10 (2006), 277-316.
Référence MathSciNet : MR2247923   DOI:10.1051/ps:2006012
Résumé    Article

       We study the probability distribution of the location of a particle performing a cyclic random motion in \(\mathbb{R}^d\). The particle can take \(n\) possible directions with different velocities and the changes of direction occur at random times. The speed-vectors as well as the support of the distribution form a polyhedron (the first one having constant sides and the other expanding with time \(t\)). The distribution of the location of the particle is made up of two components: a singular component (corresponding to the beginning of the travel of the particle) and an absolutely continuous component.

       We completely describe the singular component and exhibit an integral representation for the absolutely continuous one. The distribution is obtained by using a suitable expression of the location of the particle as well as some probability calculus together with some linear algebra. The particular case of the minimal cyclic motion (\(n=d+1\)) with Erlangian switching times is also investigated and the related distribution can be expressed in terms of hyper-Bessel functions with several arguments.

Vincent Van Gogh (1853-1890) – Iris, 1889

Masquer le résumé

First hitting time and place, monopoles and multipoles for the pseudo-process driven by the equation \(\partial/\partial t=\pm\partial^N/\partial x^N\)
Electronic Journal of Probability 12 (2007), paper no. 11, 300-353.
Référence MathSciNet : MR2299920   DOI:10.1214/EJP.v12-399
Résumé    Article

       Consider the high-order heat-type equation \(\partial u/\partial t=\pm\partial^N u/\partial x^N\) for an integer \(N>2\) and introduce the related Markov pseudo-process \((X(t))_{t\ge 0}\). In this paper, we study several functionals related to \((X(t))_{t\ge 0}\): the maximum \(M(t)\) and minimum \(m(t)\) up to time \(t\); the hitting times \(\tau_a^+\) and \(\tau_a^-\) of the half lines \((a,+\infty)\) and \((-\infty,a)\) respectively. We provide explicit expressions for the distributions of the vectors \((X(t),M(t))\) and \((X(t),m(t))\), as well as those of the vectors \((\tau_a^+,X(\tau_a^+))\) and \((\tau_a^-,X(\tau_a^-))\).

John Singer Sargent (1856-1925) – Les palais Labia et San Geremia, Venise, 1913

Masquer le résumé

A stochastic continuation approach to piecewise constant reconstruction (avec M. Robini et I. Magnin, INSA Lyon)
IEEE Transactions on Image Processing 16(10) (2007), 2576-2589.
Référence MathSciNet : MR2467787   DOI:10.1109/TIP.2007.904975
Résumé

       We address the problem of reconstructing a piecewise constant 3-D object from a few noisy 2-D line-integral projections. More generally, the theory developed here readily applies to the recovery of an ideal n-D signal from indirect measurements corrupted by noise. Stabilization of this ill-conditioned inverse problem is achieved with the Potts prior model, which leads to the minimization of a discontinuous, highly multimodal cost function. To carry out this challenging optimization task, we introduce a new class of annealing-type algorithms we call stochastic continuation (SC). We first prove that, under mild assumptions, SC inherits the desirable finite-time convergence properties of generalized simulated annealing. Then, we show that SC can be successfully applied to our 3-D reconstruction problem. In addition, we look into the concave distortion acceleration method introduced for standard simulated annealing and we derive an explicit formula for choosing the free parameter of the cost function. Numerical experiments using both synthetic data and real radiographic testing data show that SC outperforms standard simulated annealing.

John Singer Sargent (1856-1925) – Venise par temps gris, 1880

Masquer le résumé

First hitting time and place for the pseudo-process driven by the equation \(\partial/\partial t=\pm\partial^N/\partial x^N\) subject to a linear drift
Stochastic Processes and their Applications 118 (2008), 1-27.
Référence MathSciNet : MR2376250   DOI:10.1016/j.spa.2007.03.009
Résumé    Article

       Consider the high-order heat-type equation \(\partial u/\partial t=(-1)^{1+N/2}\partial^N u/\partial x^N\) for an even integer \(N>2\) and introduce the related Markov pseudo-process \((X(t))_{t\ge 0}\). Let us define the drifted pseudo-process \((X^b(t))_{t\ge 0}\) by \(X^b(t)=X(t)+bt\). In this paper, we study the following functionals related to \((X^b(t))_{t\ge 0}\): the maximum \(M^b(t)\) up to time \(t\); the first hitting time \(\tau_a^b\) of the half line \((a,+\infty)\); the hitting place \(X^b(\tau_a^b)\) at this time. We provide explicit expressions for the Laplace-Fourier transforms of the distributions of the vectors \((X^b(t),M^b(t))\) and \((\tau_a^b,X^b(\tau_a^b))\), from which we deduce remarkable expressions for the distribution of \(X^b(\tau_a^b)\) as well as for the escape pseudo-probability: \(P\{\tau_a^b=+\infty\}\).

John Singer Sargent (1856-1925) – Rio dei Mendicanti, Venise, 1909

Masquer le résumé

A note on Spitzer identity for random walk
Statistics and Probability Letters 78 (2008), 2576-2589.
Référence MathSciNet : MR2382062   DOI:10.1016/j.spl.2007.05.025
Résumé    Article

       Let \((S_n)_{n\ge 0}\) be a random walk evolving on the real line and introduce the first hitting time of the half-line \((a,+\infty)\) for any real \(a\): \(\tau_a=\min\{n\ge 1:S_n>a\}\). The classical Spitzer identity (1960) supplies an expression for the generating function of the couple \((\tau_0,S_{\tau_0})\). In (1998), Nakajima [Kodai Math. J. 21, 192-200] derived a relationship between the generating functions of the random couples \((\tau_0,S_{\tau_0})\) and \((\tau_a,S_{\tau_a})\) for any positive number \(a\). In this note, we propose a new and shorter proof for this relationship and complement this analysis by considering the case of an increasing random walk. We especially investigate the Erlangian case and provide an explicit expression for the joint distribution of \((\tau_a,S_{\tau_a})\) in this situation.

John Singer Sargent (1856-1925) – Entrée du Grand Canal, Venise, 1907

Masquer le résumé

Some Darling-Siegert relationships connected with random flights (avec V. Cammarota et E. Orsingher, Università di Roma “La Sapienza”)
Statistics and Probability Letters 79(2) (2009), 243-254.
Référence MathSciNet : MR2483547   DOI:10.1016/j.spl.2008.08.002
Résumé    Article

       We derive in detail four important results on integrals of Bessel functions from which three combinatorial identities are extracted. We present the probabilistic interpretation of these identities in terms of different types of random walks, including asymmetric ones. This work extends the results of a previous paper concerning the Darling-Siegert interpretation of similar formulas emerging in the analysis of random flights.

Ippolito Caffi (1809-1866) – Rome, vue des trous avec la colonne de Traiano

Masquer le résumé

Chung's law for homogeneous Brownian functionals (avec T. Simon, Université d'Évry)
Rocky Mountain Journal of Mathematics 40(2) (2010), 561-579.
Référence MathSciNet : MR2646458   DOI:10.1216/RMJ-2010-40-2-561
Résumé    Article

       Consider the first exit time \(T_{a,b}\) from a finite interval \([-a,b]\) for an homogeneous fluctuating functional \(X\) of a linear Brownian motion. We show the existence of a finite positive constant \(\kappa\) such that \[\lim_{t\to\infty}t^{-1}\log \mathbb{P}[ T_{ab}> t]\; =\; -\kappa.\] Following Chung's original approach [1], we deduce a “liminf” law of the iterated logarithm for the two-sided supremum of \(X\). This extends and gives a new point of view on a result of Khoshnevisan and Shi [2].

[1] K. L. Chung. On the maximum partial sums of sequences of independent random variables. Trans. Amer. Math. Soc. 64 (1948), 205-233.

[2] D. Khoshnevisan and Z. Shi. Chung's law for integrated Brownian motion. Trans. Amer. Math. Soc. 350(10) (1998), 4253-4264.

Francesco Guardi (1712-1793) – Santa Maria della Salute, 1783

Masquer le résumé

Joint distribution of the process and its sojourn time in the positive half-line for pseudo-processes governed by higher-order heat-type equations (avec V. Cammarota, Università di Roma “La Sapienza”)
Electronic Journal of Probability 15 (2010), Paper no. 28, 895-931.
Référence MathSciNet : MR2653948   DOI:10.1214/EJP.v15-782
Résumé    Article

       Consider the high-order heat-type equation \(\partial u/\partial t=\pm\,\partial^N u/\partial x^N\) for an integer \(N>2\) and introduce the related Markov pseudo-process \((X(t))_{t\ge 0}\). In this paper, we study the sojourn time \(T(t)\) in the positive half-line \([0,+\infty)\) up to a fixed time \(t\) for this pseudo-process. We provide explicit expressions for the joint distribution of the couple \((T(t),X(t))\).

Ippolito Caffi (1809-1866) – Rome, avec vue sur le Tibre, Castel Sant'Angelo et Saint-Pierre

Masquer le résumé

A class of bridges of iterated integrals of Brownian motion related to various boundary value problems involving the one-dimensional polyharmonic operator
International Journal of Stochastic Analysis 2011 (2011), Art. ID 762486, 32 p.
Référence MathSciNet : MR2861121   DOI:10.1155/2011/762486
Résumé    Article

       Let \((B(t))_{t\in [0,1]}\) be the linear Brownian motion and \((X_n(t))_{t\in [0,1]}\) be the \((n-1)\)-fold integral of Brownian motion, \(n\) being a positive integer: \[X_n(t)=\int_0^t \frac{(t-s)^{n-1}}{(n-1)!} \,\mathrm{d} B(s) \text{ for any } t\in[0,1].\] In this paper we construct several bridges between times \(0\) and \(1\) of the process \((X_n(t))_{t\in [0,1]}\) involving conditions on the successive derivatives of \(X_n\) at times \(0\) and \(1\). For this family of bridges, we make a correspondance with certain boundary value problems related to the one-dimensional polyharmonic operator. We also study the classical problem of prediction. Our results involve various Hermite interpolation polynomials.

Emmanuel Costa (1833-1921) – Le monastère de Saint-Pons

Masquer le résumé

A random walk model related to the clustering of membrane receptors
In: Skogseid, A. and Fasano, V. (eds) “Statistical Mechanics and Random Walks: Principles, Processes and Applications”, Chapter 18, 545-580, Nova Science publishers, 2012.
Résumé    Article

       In a cellular medium, the plasmic membrane is a place of interactions between the cell and its direct external environment. A classic model describes it as a fluid mosaic. The fluid phase of the membrane allows a lateral degree of freedom to its constituents: they seem to be driven by random motions along the membrane. On the other hand, experimentations bring to light inhomogeneities on the membrane; these micro-domains (the so-called rafts) are very rich in proteins and phospholipids. Nevertheless, few functional properties of these micro-domains have been shown and it appears necessary to build appropriate models of the membrane for recreating the biological mechanism.

       In this article, we propose a random walk model simulating the evolution of certain constituents–the so-called ligands–along a heterogeneous membrane. Inhomogeneities–the rafts–are described as being still clustered receptors. An important variable of interest to biologists is the time that ligands and receptors bind during a fixed amount of time. This stochastic time can be interpreted as a measurement of affinity/sentivity of ligands for receptors. It corresponds to the sojourn time in a suitable set for a certain random walk.

       We provide a method of calculation for the probability distribution of this random variable and we next determine explicitly this distribution in the simple case when we are dealing with only one ligand and one receptor. We finally address some further more realistic models.

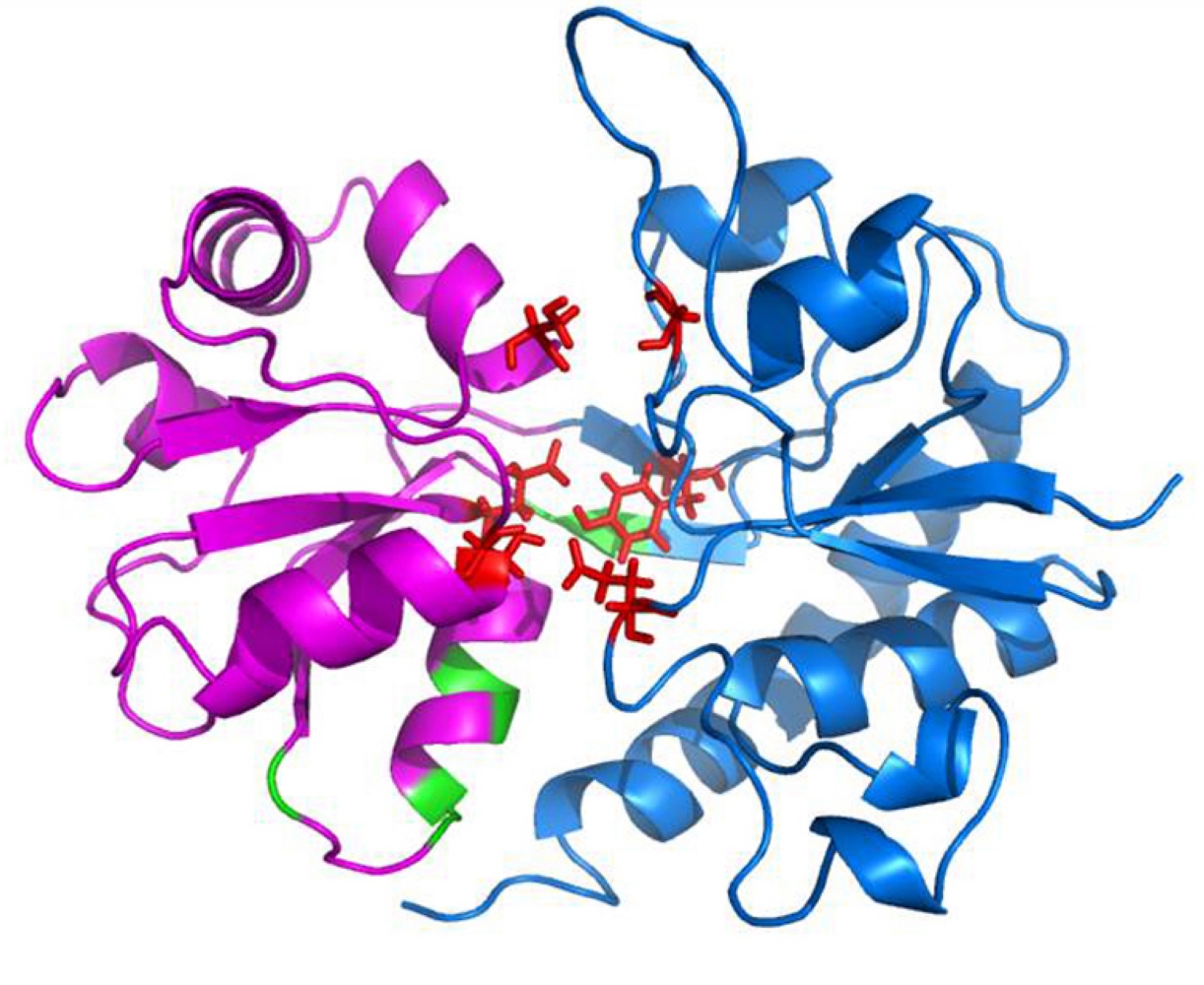
Structure d'un domaine de liaison ligand-récepteur du glutamate mettant en évidence des résidus (rouge) qui font connexion à travers la fente. Le résidu central forme une liaison stabilisant le domaine dans un état fermé.

Masquer le résumé

Sojourn time in \(\mathbb{Z}^+\) for the Bernoulli random walk on \(\mathbb{Z}\)
ESAIM: Probability and Statistics 16 (2012), 324-351.
Référence MathSciNet : MR2966167   DOI:10.1051/ps/2010013
Résumé    Article

       Let \((S_k)_{k\ge 1}\) be the classical Bernoulli random walk on the integer line with jump parameters \(p\in(0,1)\) and \(q=1-p\). The probability distribution of the sojourn time of the walk in the set of non-negative integers up to a fixed time is well-known, but its expression is not simple. By modifying slightly this sojourn time–through a particular counting process of the zeros of the walk as done by Chung and Feller ["On fluctuations in coin-tossings", Proc. Nat. Acad. Sci. U.S.A. 35 (1949), 605-608]–, simpler representations may be obtained for its probability distribution. In the aforementioned article, only the symmetric case (\(p=q=1/2\)) is considered. This is the discrete counterpart to the famous Paul Lévy's arcsine law for Brownian motion.

Francesco Guardi (1712-1793) – Le Grand Canal, avec les églises San Simeone et Santa Lucia, 1780

Masquer le résumé

Joint distribution of the process and its sojourn time in a half-line \([a,+\infty)\) for pseudo-processes governed by higher-order heat-type equations (avec V. Cammarota, Università di Roma “La Sapienza”)
Stochastic Processes and their Applications 122 (2012), 217-249.
Référence MathSciNet : MR2860448   DOI:10.1016/j.spa.2011.08.004
Résumé    Article

       Let \((X(t))_{t \ge 0}\) be the pseudo-process driven by the high-order heat-type equation \(\partial u/\partial t=\pm\,\partial^N u/\partial x^N\), where \(N\) is an integer greater than 2. Let us introduce the sojourn time spent by \((X(t))_{t \ge 0}\) in \([a,+\infty)\) (\(a\in \mathbb{R}\)), up to a fixed time \(t>0\): \(T_a(t)=\int_0^t 1\!\!\mathrm{l}_{[a,+\infty)}(X(s))\,\mathrm{d}s\). The purpose of this paper is to explicit the joint pseudo-distribution of the vector \((T_a(t),X(t))\) when the pseudo-process starts at a point \(x\in \mathbb{R}\) at time \(0\). The method consists of solving a boundary value problem satisfied by the Laplace transform of the aforementioned distribution.

Ippolito Caffi (1809-1866) – Vue de Santa Maria Maggiore et Santa Prassede

Masquer le résumé

A survey on the pseudo-process driven by the high-order heat-type equation \(\partial/\partial t=\pm\partial^N/\partial x^N\) concerning the first hitting times and sojourn times
Methodology and Computing in Applied Probability 14(3) (2012), 549-566.
Référence MathSciNet : MR2966309   DOI:10.1007/s11009-011-9245-8
Résumé    Article

       Fix an integer \(n>2\) and let \((X(t))_{t\ge 0}\) be the pseudo-process driven by the high-order heat-type equation \(\partial/\partial t=\pm\partial^n/\partial x^n\). The denomination ''pseudo-process'' means that \((X(t))_{t\ge 0}\) is related to a signed measure (which is not a probability measure) with total mass equal to 1.

In this note, we present some results and discuss some problems concerning the pseudo-distributions of the first overshooting times of a single barrier \(\{a\}\) or a double barrier \(\{a,b\}\) by \((X(t))_{t\ge 0}\), as well as those of the sojourn times of \((X(t))_{t\ge 0}\) in the intervals \([a,+\infty)\) and \([a,b]\) up to a fixed time.

Emmanuel Costa (1833-1921) – La cathédrale Saint-Nicolas à Nice

Masquer le résumé

Sojourn time in an union of intervals for diffusions
Methodology and Computing in Applied Probability 15(4) (2013), 743-771.
Référence MathSciNet : MR3117625   DOI:10.1007/s11009-012-9280-0
Résumé    Article

       We give a method for computing the iterated Laplace-transform of the sojourn time in an union of intervals for linear diffusion processes. This random variable comes from a model occurring in biology concerning the clustering of membrane receptors. The way used hinges on solving differential equations. Masquer le résumé

From pseudo-random walk to pseudo-Brownian motion: first exit time from a one-sided or a two-sided interval
International Journal of Stochastic Analysis 2014 (2014), Art. ID 520136, 49 p.
Référence MathSciNet : MR3191097   DOI:10.1155/2014/520136
Résumé    Article

       Let \(N\) be a positive integer, \(c\) be a positive constant and \((U_n)_{n\ge 1}\) be a sequence of independent identically distributed pseudo-random variables. We assume that the \(U_n\)'s take their values in the discrete set \(\{-N,-N+1,\dots,N-1,N\}\) and that their common pseudo-distribution is characterized by the (positive or negative) real numbers \[\mathbb{P}\{U_n=k\}=\delta_{k0}+(-1)^{k-1} c{2N\choose k+N}\] for any \(k\in\{-N,-N+1,\dots,N-1,N\}\). Let us finally introduce \((S_n)_{n\ge 0}\) the associated pseudo-random walk defined on \(\mathbb{Z}\) by \(S_0=0\) and \(S_n=\sum_{j=1}^n U_j\) for \(n\ge 1\).

In this paper, we exhibit some properties of \((S_n)_{n\ge 0}\). In particular, we explicitly determine the pseudo-distribution of the first overshooting time of a given threshold for \((S_n)_{n\ge 0}\) as well as that of the first exit time from a bounded interval.

Next, with an appropriate normalization, we pass from the pseudo-random walk to the pseudo-Brownian motion driven by the high-order heat-type equation \(\partial/\partial t=(-1)^{N-1} c\;\partial^{2N}\!/\partial x^{2N}\). We retrieve the corresponding pseudo-distribution of the first overshooting time of a threshold for the pseudo-Brownian motion (Lachal, A.: First hitting time and place, monopoles and multipoles for pseudo-processes driven by the equation \(\partial/\partial t=\pm \partial^N/\partial x^N\). Electron. J. Probab. 12 (2007), 300-353 [MR2299920]). In the same way, we get the pseudo-distribution of the first exit time from a bounded interval for the pseudo-Brownian motion which is a new result for this pseudo-process.

Vincent Van Gogh (1853-1890) – Amandier en fleurs, 1890

Masquer le résumé

First exit time from a bounded interval for pseudo-processes driven by the equation \(\partial/\partial t=(-1)^{N-1} \partial^{2N}\!/\partial x^{2N}\)
Stochastic Processes and their Applications 124(2) (2014), 1084-1111.
Référence MathSciNet : MR3138608   DOI:10.1016/j.spa.2013.09.016
Résumé    Article

       Let \(N\) be a positive integer. We consider pseudo-Brownian motion \(X=(X(t))_{t \ge 0}\) driven by the high-order heat-type equation \(\partial/\partial t=(-1)^{N-1} \partial^{2N}\!/\partial x^{2N}\). Let us introduce the first exit time \(\tau_{ab}\) from a bounded interval \((a,b)\) by \(X\) (\(a,b\in \mathbb{R}\)) together with the related location, namely \(X_{\tau_{ab}}\).

In this paper, we provide a representation of the joint pseudo-distribution of the vector \((\tau_{ab},X(\tau_{ab}))\) by means of some determinants. The method we use is based on the Feynman-Kac functional related to pseudo-Brownian motion which leads to a boundary value problem. In particular, the pseudo-distribution of \(X(\tau_{ab})\) admits a fine expression involving famous Hermite interpolating polynomials.

Federico Moja (1802–1885) – La cour du palais des Doges, Venise

Masquer le résumé

Entrance and sojourn times for Markov chains. Application to \((L,R)\)-random walks (avec V. Cammarota, Università di Roma “Tor Vergata”)
Markov Processes and Related Fields 21(4) (2015), 887-938.
MathSciNet reference: MR3496230
Résumé    Article

       In this paper, we provide a methodology for computing the probability distribution of certain sojourn times for Markov chains. Our methodology hinges on matrix equations for various generating functions. As an example, we apply this methodology to a class of random walks with bounded integer-valued jumps.

Giovanni Paolo Panini (1691–1765) – Caprice avec le Colisée, 1735

Masquer le résumé

Some asymptotic results for the integrated empirical process with applications to statistical tests (avec S. Alvarez-Andrade et S. Bouzebda, Université de Technologie de Compiègne)
Communications in Statistics – Theory and Methods 46(7) (2017), 3365-3392
MathSciNet reference: MR3589103   DOI:10.1080/03610926.2015.1060346
Résumé    Article

       The main purpose of this paper is to investigate the strong approximation of the integrated empirical process. More precisely, we obtain the exact rate of the approximations by a sequence of weighted Brownian bridges and a weighted Kiefer process. Our arguments are based in part on the Komlós et al.'s results, [1]. Applications include the two-sample testing procedures together with the change-point problems. We consider also the strong approximation of the integrated empirical process when the parameters are estimated. Finally, we study the behavior of the self-intersection local time of the partial sums process representation of the integrated empirical process.

[1] Komlós, J., Major, P. and Tusnády, G. An approximation of partial sums of independent RV's and the sample DF (I). Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 32 (1975), 111-131.

Carle Vernet – Napoléon à la chasse dans la forêt de Compiègne, 1811

Masquer le résumé

Strong approximations for the \(p\)-fold integrated empirical processes with applications to statistical tests (avec S. Alvarez-Andrade et S. Bouzebda, Université de Technologie de Compiègne)
TEST 27(4) (2018), 826-849
MathSciNet reference: MR3878363   DOI:10.1007/s11749-017-0572-0
Résumé    Article

       The main purpose of this paper is to investigate the strong approximation of a class of integrated empirical processes. More precisely, we obtain the exact rate of the approximations by a sequence of weighted Brownian bridges and a weighted Kiefer process. Our arguments are based in part on the Komlós et al.'s results, [1]. Applications include the two-sample testing procedures together with the change-point problems. We also consider the strong approximation of integrated empirical processes when the parameters are estimated.

[1] Komlós, J., Major, P. and Tusnády, G. An approximation of partial sums of independent RV's and the sample DF (I). Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 32 (1975), 111-131.

Raymond Fournier-Sarlovèze (1836-1916) – 23 mai 1430, Prise de Jeanne d'Arc devant Compiègne

Masquer le résumé

Sur l'intégrale du mouvement brownien
t. 311 (1990), 461-464.   Référence MathSciNet : MR1075671 (91i:60207)
Résumé

       Let \((B_t)_{t\ge0}\), be the standard Brownian motion in \(\mathbb{R}\). Define \(X_t=\int^t_0B_s\,ds\), \(U_t=(X_t+x+ty,B_t+y)\), \((x,y) \in\mathbb{R}^2\), and \(\tau_a=\inf\{t>0\); \(U_t\in\{a\}\times\mathbb{R}\}\). In this note we compute explicitly the joint distribution of \(\tau_a\) and \(U_{\tau_a}\). We also indicate a simple proof of a recent result of M. Lefebvre with some improvements.

Edouard Manet (1832-1883) – Le banc (le jardin de Versailles), 1880-81

Masquer le résumé

Sur les excursions de l'intégrale du mouvement brownien
t. 314 (1992), 1053-1056.   Référence MathSciNet : MR1168534 (93c:60123)
Résumé

       Let \((B(t))_{t\ge 0}\) be the standard Brownian motion in \(\mathbb{R}\) started at \(0\), and let \(X(t)=\int^t_0 B(s)\,ds+x+ty\), where \((x,y)\in\mathbb{R}^2\) is a fixed point. In this note we compute explicitly the law of the excursion process straddling a fixed instant \(T>0\) related to \((X(t))_{t\ge 0}\).

Pierre-Auguste Renoir (1841-1919) – Rochers à l'Estaque, 1882

Masquer le résumé

Sur les temps de passages successifs de l'intégrale du mouvement brownien
t. 321 (1995), 903-908.   Référence MathSciNet : MR1355850 (96k:60207)
Résumé

       Dans cette note nous explicitons diverses distributions associées aux temps de passages successifs en 0 pour l'intégrale du mouvement brownien.

Jean-Baptiste Camille Corot (1796-1875) – Vue de Gênes, 1834

Masquer le résumé

Temps de sortie d'un intervalle borné pour la primitive du mouvement brownien
t. 324 (1997), 559-564.   Référence MathSciNet : MR1443994 (98a:60116)   DOI:10.1016/S0764-4442(99)80390-5
Résumé

       Let \((B_t)_{t\ge0}\) be a standard Brownian motion starting at \(y, X_ t=x+\int^t_0B_sds, x\in(a,b)\). Set \(\tau_{ab}=\inf\{t>0\colon X_ t\notin(a,b)\}\). In this paper, we compute the moments of the random variable \(B_{\tau_{ab}}\), and deduce the probability law of \(B_{\tau_{ab}}\). We show how to obtain the expectation \({\bf E}_{(x,y)}(\tau^m_ {ab}B^n_{\tau_{ab}}\)). We also determine explicitly the probabilities \({\bf P}_{(x,y)}\{X_{\tau_{ab}}=a\}\) and \({\bf P}_{(x,y)}\{X_{\tau_{ab}}=b\}\).

Henri Fantin-Latour (1836-1904) – Nature morte aux fleurs, 1881

Masquer le résumé

Quelques lois de probabilités associées à un modèle de duplication d'un ADN
t. 336 (2003), 175-180.   Référence MathSciNet : MR1969574 (2004c:62030)   DOI:10.1016/S1631-073X(03)00006-2
Résumé   Article

       Dans cette Note, on calcule explicitement les transformées de Laplace de plusieurs variables aléatoires introduites par Cowan and Chiu dans un modèle probabiliste du processus de duplication d'un ADN, [1] et [2]. Ces transformées de Laplace s'obtiennent à partir d'équations de quasi-renouvellement ou d'équations différentielles fonctionnelles et sont exprimées au moyen de produits infinis issus de la théorie des partitions.

[1] R. Cowan. Stochastic models for DNA replication, in The Handbook of Statistics, Vol. 20, eds. C.R. Rao and D.N. Shanbhag, Elsevier, 2001.

[2] R. Cowan and S.N. Chiu. Stochastic model of fragment formation when DNA replicates, J. Appl. Prob. 31 (1994), 301-308.

Paul Cézanne (1839-1906) – La Montagne Sainte-Victoire, 1885

Masquer le résumé

Lois conjointes du processus et de son maximum, des premier instant et position d'atteinte d'une demi-droite pour le pseudo-processus régi par l'équation \(\partial/\partial t=\pm\partial^n/\partial x^n\)
t. 343 (2006), 525-530.   Référence MathSciNet : MR2267588   DOI:10.1016/j.crma.2006.09.027
Résumé   Article

       Dans cette Note, on présente des formules explicites pour les distributions conjointes du pseudo-processus régi par l'équation \(\frac{\partial}{\partial t}=\pm\frac{\partial^N}{\partial x^N}\) couplé avec son maximum, et du premier instant de dépassement d'un seuil fixé par ce pseudo-processus couplé avec sa position relative à cet instant.

John Singer Sargent (1856-1925) – Rio dell'Angelo

Masquer le résumé

La pyramide de Kheops et quelques équations du quatrième degré
Quadrature 69 (2008), 36-47.   Référence Zentralblatt MATH : Zbl 1242.51013   DOI:10.1051/quadrature:2008004
Résumé    Article

       Dans un article publié dans l'édition française de la revue australienne Nexus, James Colmer présentait une hypothèse originale sur la fonction de la pyramide de Kheops et sur l'existence présumée d'un ensemble de galeries et chambres cachées, symétriques à celles connues. La démarche de J. Colmer, dans sa recherche, passait par un tracé géométrique impliquant un certaine valeur de l'angle formé par la face de la pyramide avec sa base horizontale et la triple intersection d'une circonférence avec deux segments de droites spécifiques.

       André Dufour, traducteur pour Nexus France et architecte de métier, ayant eu la charge de traduire cet article, s'aperçut après avoir refait sur ordinateur le tracé géométrique de J. Colmer que ce dernier était faux. Cela n'enlevait rien à l'intérêt de l'hypothèse de J. Colmer, objet principal de l'article, mais posait un problème intéressant de géométrie. Après en avoir fait une note de traducteur publiée simultanément avec l'article traduit de J. Colmer, plusieurs lecteurs, F. De Ligt, J.-F. Pioche et l'auteur du présent article réagirent au problème en fournissant des valeurs exactes pour l'angle mis en cause par le biais de diverses méthodes calculatoires.

       Par une démarche empirique, A. Dufour tenta une construction graphique à l'aide d'un logiciel de dessin vectoriel afin d'obtenir la position du sommet de la pyramide requise par la théorie de J. Colmer. Cette approche, qu'il a soumise à l'auteur, repose sur la construction d'une courbe en polyligne lissée dont l'intersection avec une droite adéquate fournit avec une excellente précision la position du sommet recherché (en fait deux sommets conviendront comme cela apparaîtra ultérieurement). Par une approche analytique, l'auteur prouvera alors que cette construction est parfaitement exacte. Il est intéressant de noter que, bien au-delà d'un exercice de géométrie élémentaire en apparence, ce problème suscitera en fait une analyse mathématique particulièrement riche touchant à des domaines diversifiés.

       Tous les éléments des diverses correspondances entre A. Dufour, F. De Ligt, J.-F. Pioche et l'auteur sont rassemblées dans le présent article.

David Roberts (1796-1864) – Les pyramides de Khéops et Khéphren

Masquer le résumé

Mélanges parfaits de cartes (I). In-shuffles et out-shuffles
Quadrature 76 (2010), 13-25.   Référence Zentralblatt MATH : Zbl 1214.91014   DOI:10.1051/quadrature/2010001
Résumé    Article

       Dans cet article suivi d'un article compagnon qui paraîtra dans le prochain numéro de Quadrature, on étudie quelques mélanges de cartes bien connus du monde de la magie. On examine en détail l'éventualité de reconstituer le jeu de cartes initial après plusieurs mélanges consécutifs. Il s'agit mathématiquement d'un problème de systèmes dynamiques discrets pour lequel on recherche explicitement une période. Les calculs reposant sur des considérations algébriques élémentaires, l'article se veut accessible à un large public.

Paul Cézanne (1839-1906) – Les joueurs de cartes, 1890-1892

Masquer le résumé

Mélanges parfaits de cartes (II). Mélanges de Monge
Quadrature 77 (2010), 23-29.   Référence Zentralblatt MATH : Zbl 1262.91038   DOI:10.1051/quadrature/2010008
Résumé    Article

       Dans cet article qui fait suite à un travail paru dans le numéro précédent de Quadrature, on s'intéresse à une classe de mélanges de cartes – appelés mélanges de Monge – bien connus du monde de la magie. On étudie la possibilité de retrouver le jeu de cartes initial après plusieurs mélanges successifs. Il s'agit d'un problème de systèmes dynamiques discrets pour lequel on recherche explicitement une période. L'approche adoptée ici est élémentaire, ce qui rend l'article facilement abordable.

Paul Cézanne (1839-1906) – Les joueurs de cartes, 1890-1892

Masquer le résumé

Cartomagie : principes de Gilbreath (I). Dénombrement de mélanges américains (avec P. Schott, ESIEA de Paris)
Quadrature 85 (2012), 24-35.   Référence Zentralblatt MATH : Zbl 06131689
Résumé    Article

       Les principes magiques de Gilbreath permettent, à partir d'un jeu de cartes préalablement classé après un mélange américain, de garder ses propriétés de classement par bloc de cartes mais de façon éventuellement désordonnée (les cartes d'un même bloc n'étant plus dans l'ordre du classement initial). De telles propriétés permettent de voir se réaliser des prédictions malgré un vrai mélange ! Nous exposons en trois parties ces principes de cartomagie. Dans ce premier volet, nous présentons les mélanges américains et détaillons leur dénombrement. Dans deux autres volets, nous présenterons des applications magiques des principes de Gilbreath, ainsi que leur démonstration mathématique.

Adriaen Brouwer (1605-1638) – Les joueurs de cartes

Masquer le résumé

Cartomagie : principes de Gilbreath (II). Quelques applications (avec P. Schott, ESIEA de Paris)
Quadrature 86 (2012), 31-37.   Référence Zentralblatt MATH : Zbl 1254.97015     Référence MathSciNet : MR3059190
Résumé    Article

       Les principes magiques de Gilbreath permettent, à partir d'un jeu de cartes préalablement classé de garder, après un mélange américain, ses propriétés de classement par bloc de cartes mais de façon éventuellement désordonnée (les cartes d'un même bloc n'étant plus dans l'ordre du classement initial). De telles propriétés permettent de voir se réaliser des prédictions malgré un vrai mélange ! Nous avons proposé dans un premier volet paru dans le numéro précédent de Quadrature un calcul de dénombrement des mélanges américains possibles ainsi qu'un algorithme permettant de les réaliser à partir d'un jeu de cartes donné. Dans ce second volet, nous donnons des applications des mélanges américains fondées sur les principes magiques de Gilbreath. Pour chacun d'entre eux, nous présentons un tour de magie. Les démonstrations de ces principes font l'objet d'un dernier volet qui apparaîtra dans le prochain numéro.

Michelangelo Merisi da Caravaggio (1571-1610) – Les tricheurs, 1594

Masquer le résumé

Cartomagie : principes de Gilbreath (III). Diverses démonstrations (avec P. Schott, ESIEA de Paris)
Quadrature 87 (2013), 30-37.   Référence Zentralblatt MATH : Zbl 1284.00003     Référence MathSciNet : MR3059800
Résumé    Article

       Les principes magiques de Gilbreath permettent, à partir d'un jeu de cartes préalablement classé de garder, après un mélange américain, ses propriétés de classement par bloc de cartes mais de façon éventuellement désordonnée (les cartes d'un même bloc n'étant plus dans l'ordre du classement initial). De telles propriétés permettent de voir se réaliser des prédictions malgré un vrai mélange ! Nous avons proposé dans deux volets parus dans les numéros précédents de Quadrature un calcul de dénombrement des mélanges américains possibles ainsi que plusieurs tours de magie reposant sur les principes magiques de Gilbreath. Dans ce dernier volet, nous fournissons les démonstrations détaillées de chacun de ces principes.

Georges de La Tour (1593-1652) – Le tricheur à l'as de carreau, 1632

Masquer le résumé

Un tour de magie autour de Fibonacci, Lucas et Chebyshev
Quadrature 93 (2014), 27-35.     Référence MathSciNet : MR3237161
Résumé    Article

       Nous présentons un tour de magie autour des nombres de Fibonacci que l'on peut trouver dans divers manuels de magie. Ce tour consiste à calculer rapidement la somme des termes successifs d'une suite de type Fibonacci. Nous fournissons des explications ainsi que des extensions de cette astuce pour des suites plus générales. Cette étude nous a conduit à des connexions intéressantes entre les suites de Fibonacci, de Lucas et les polynômes de Tchebychev.

Leonardo Fibonacci (1175-1250)

Masquer le résumé

Quelques modèles de reproduction stochastiques
Document

Modèles phylogénétiques stochastiques
Document

Alignement de séquences : modèles stochastiques
Document

Bridges of certain Wiener integrals: some properties and application to goodness-of-fit testing
Fourth Hungarian Colloquium on limit theorems of Probability and Statistics, Balatonlelle (Hongrie) et séminaire d'Aarhus (Danemark), 1999
Exposé

Étude de quelques nouvelles statistiques intégrées
Journées de probabilités, Luminy, 2000
Exposé

Quelques modèles probabilistes en biologie moléculaire
Séminaire de Dijon, 2002
Exposé

Lois du temps de séjour et du maximum pour un pseudo-processus gouverné par l'équation de la chaleur d'ordre supérieur \(\partial u/\partial t = \pm\partial^n u/\partial x^n\)
Séminaire de Nancy, 2002
Exposé

Un modèle de réplication d'un ADN
Séminaire de Saint-Étienne, 2003
Exposé

Quelques problèmes de temps de passage pour certains processus non nécessairement markoviens
Journées SMAI : Modélisation aléatoire et statistique, Nancy, 2004
Exposé

Maximum, first hitting time and first hitting place of a half-line for a pseudo-process driven by a high-order heat-type equation
Séminaire de Rome (Italie), 2006
Exposé

Un panorama de lois remarquables pour le pseudo-processus régi par l'équation de type chaleur \(\partial u/\partial t=\pm\partial^nu/\partial x^n\) d'ordre \(n>2\)
Séminaire d'Évry, 2008
Exposé

A survey on the pseudo-process driven by the high-order heat-type equation \(\partial/\partial t=\pm\partial^N/\partial x^N\) concerning the first hitting times and sojourn times
Fifth International Workshop on Applied Probability, Madrid (Espagne), 2010
Exposé

Some stochastic processes related to the polyharmonic differential operator
Self-Similarity and Stochastic Analysis, le Touquet, 2011
Exposé

Mouvement brownien, pseudo-mouvement brownien et EDP. Applications
Journées Modélisation Mathématique et Calcul Scientifique, Sainte Foy-lès-Lyon, 2011
Exposé

Mathémagie : Une approche didactique des mathématiques et des sciences par la Magie (avec P. Schott, ESIEA de Paris)
Cycle de conférences mathématiques, Insa de Lyon, 2012
Exposé : Présentation - Une vidéo

Pseudo-marche aléatoire et pseudo-mouvement brownien : premier instant de dépassement d'un seuil simple ou double
Séminaire de Lille, 2014
Exposé

Panorama sur l'intégrale du mouvement brownien et autres processus intégrés
Séminaire de Lille, 2014
Exposé

Entrance and sojourn times for Markov chains. Application to \((L,R)\)-random walks
A probability afternoon, Lille, 2015
Stochastic processes under constraints, Augsburg (Allemagne), 2016
Exposé

Some distributions on pseudo-Brownian motion and pseudo-random walk
Recent developments in probability theory and stochastic processes – A conference in honour of Enzo Orsingher on the occasion of his 70th birthday, Rome (Italie), 2016
Exposé

Math&Magie (II) : Les Mathématiques au service de la Magie ou la Magie au service des Mathématiques ? (avec P. Schott, ESIEA de Paris)
Cycle de conférences mathématiques, Insa de Lyon, 2016
Exposé : Partie 1 - Partie 2

Carrés magiques, cartomagie (avec P. Schott, ESIEA de Paris)
Exposition «Magimatique», Maison des Mathématiques et de l'Informatique, Lyon, 2016/2017
Matériel : Diaporama - Poster 1 - Poster 2 - Poster 3 - Poster 4

Math&Magie (III) : La Mathématique est-elle Magique ? ou la Magie est-elle Mathématique ? (avec P. Schott, ESIEA de Paris)
Exposition «Magimatique», Maison des Mathématiques et de l'Informatique, Lyon, 2017
Exposé

Some asymptotic results for integrated empirical processes with applications to statistical tests
10th International Conference of the ERCIM WG on Computational and Methodological Statistics, London (Royaume-Uni), 2017
Exposé

Math&Magie (IV) : La Mathématique est-elle Magique ? ou la Magie est-elle Mathématique ? (avec P. Schott, ESIEA de Paris)
Cycle de conférences mathématiques, Insa de Lyon, 2018
Exposé

Mélanges Faros et cryptographie
Rallye mathématique de l’académie de Lyon, Insa Lyon, 2023
Exposé

Accueil Curriculum vitæ Enseignement Recherche

Vincent Van Gogh (1853-1890) – La nuit étoilée, 1889