


|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
16
| Les élèves de troisième, munis du théorème de Pythagore et des identités remarquables, pourront résoudre le problème à l'aide d'une petite équation.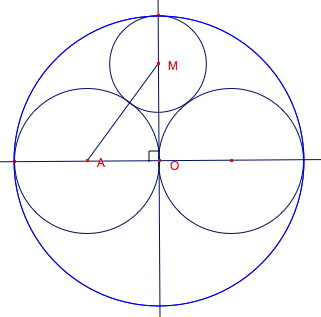
Appelons x le rayon du petit cercle. La construction de la figure est un problème en soi, qui peut être proposé après le calcul, comme application du théorème de Thalès. |
17
| Dans le même style que le précédent. Les données facilitent le calcul. En notant x le rayon de la petite boule, on a OC=5x et AC=3x, d'où OA=4x. On en déduit que le côté de la boîte est 9x |