


|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
24
Construire la bissectrice de l'angle formé par les deux droites. |
Dans ce type de problème, il est important d'expliquer aux élèves que la consigne « sans sortir du cadre » est une contrainte portant sur la construction à trouver, mais qui ne s'applique pas aux tracés qu'ils peuvent effectuer pendant leur recherche. L'important est que l'on ne doit pas utiliser le point d'intersection des deux droites dans la construction finale. Le problème 24 a de multiples solutions. Par exemple, on peut tracer un losange dont deux côtés sont portés par les deux droites données, utiliser une transformation, symétrie ou translation de façon que les images des deux droites se coupent dans le cadre... Voici une construction utilisant deux triangles ayant en commun la bissectrice cherchée.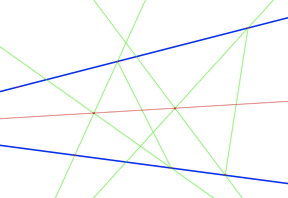
| ||||
25
Les deux droites se coupent en I. | Le problème 25 a également beaucoup de solutions On peut construire un triangle de sommet M dont les deux droites données sont médiatrices, ou hauteurs, un parallélogramme de centre M, des symétriques des deux droites se coupant à l'intérieur du cadre, etc.
|