


|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
8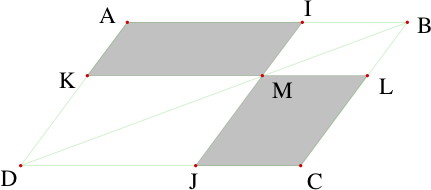
ABCD est un parallélogramme. M est un point quelconque de la diagonale [BD]. (IJ) et (KL) sont parallèles aux côtés de ABCD. Compare l'aire des deux parallélogrammes grisés. |
En situation papier-crayon, les élèves font des mesures, dans différents cas, ce qui peut laisser un certain doute quand au résultat. Avec un LGD, la conjecture est immédiate et difficile à mettre en doute. Il est plus intéressant de poser le problème sous une autre forme, par exemple, en laissant le point M libre : « ABCD est un parallélogramme. M est un point quelconque à l'intérieur de ce parallélogramme. (IJ) et (KL) sont parallèles aux côtés de ABCD. Où faut-il placer M pour que l'aire de AIKM soit égale à celle de MLCJ ? » 
Dans les deux cas, on attend des élèves une preuve basée sur la propriété : Signalons une série de problèmes du même type, parue dans |