irem lyon
menu
12345678910111213141516171819202122232425262728
29303132333435363738394041424344454647484950515253 545556

2


figpb2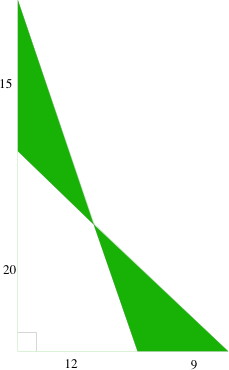

Les deux triangles hachurés ont-ils la même aire ?

Que peut-on calculer simplement ici ?
  • l'aire d'un triangle rectangle dont les côtés de l'angle droit mesurent 35 cm et 12 cm,
    soit (35x12) ÷ 2 = 210
  • et l'aire d'un autre triangle rectangle dont les côtés de l'angle droit mesurent 21 cm et 20 cm
    soit (21x20) ÷ 2 = 210.
    • Ces deux triangles ont donc la même aire.

    Si l'on enlève à chacun de ces deux triangles le quadrilatère qui forme leur intersection commune, il reste... les deux triangles « hachurés » qui ont donc la même aire.

    Une généralisation possible (difficile)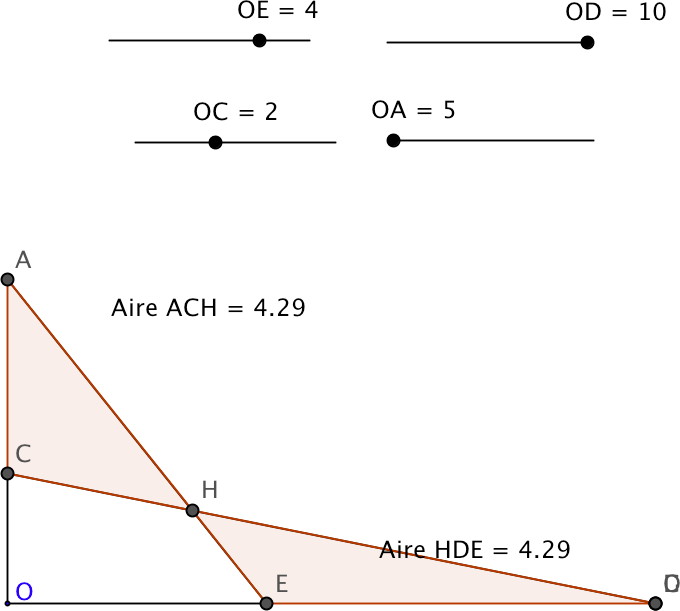
    Comment choisir les longueurs données pour obtenir l'égalité des deux aires ? Dans la figure animée ci-dessous, les longueurs OA, OC, OE, OD sont contrôlées par des curseurs de façon à limiter l'observation à quelques valeurs simples et permettre la conjecture :
    "Les triangles ACH et HDE ont la même aire si et seulement si OC.OD = OA.OE.

    animggb