


|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
4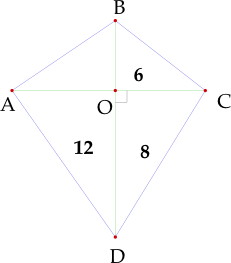 On donne les aires des triangles OBC, OCD et OAD. Trouve l'aire du triangle AOB. | ||
Tout d'abord, il est raisonnable de compléter la figure pour travailler sur des rectangles.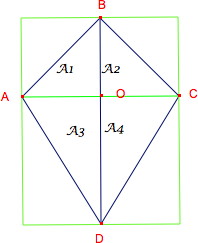 |
Solutions (qu'on n'attend pas nécessairement d'un élève de collège) Solution algébrique Utilisation d'un résultat sur les aires | Recherche des élèves Les élèves peuvent avoir l'impression au départ qu'il « manque des données », et pourtant ils peuvent trouver facilement la réponse pour peu qu'on les encourage à faire des essais. Prenons OB = 3, OC = 4. On en déduit OD = 4 puis OA = 6. Le quatrième rectangle a une aire de 18, donc l'aire cherchée est 9. Et si OB = 6 et OC = 2 ? OD = 8 et OA = 3. Tiens, on trouve la même aire au final ! On peut multiplier les essais à la calculatrice. Quelques petits malins peuvent remarquer qu'il suffit de faire le produit en croix. Dans ce cas, on leur suggère de tester d'autres valeurs pour les trois aires données. Après cette étape, l'utilisation d'un LGD est tout à fait pertinente pour conjecturer un résultat général. |