irem lyon
menu
12345678910111213141516171819202122232425262728
29303132333435363738394041424344454647484950515253 545556

30 Jouons les prolongations !

Soit un triangle ABC et un point M du côté [AC], tels que AB = 2 BC et AM = 2 MC.
Comparer les angles ABM et MBC.
On peut conjecturer que la droite BM est la bissectrice de l'angle B. Comment le prouver ?

Quand nous avons proposé ce problème, nous pensions à l'utilisation astucieuse d'une propriété des médianes du triangle.

Malheureusement l'étude des médianes du triangle n'est plus au programme du collège.
Heureusement, il y a d'autres ressources (voir les trois autres démonstrations proposées).

Le problème peut être simplement utilisé comme situation de construction puis d'exploration et de recherche de conjectures à l'aide d'un LGD. Dans ce cadre, il peut même être généralisé au cas BA/BC =AM/MC.

Théorème Dans un triangle ABC avec M sur [AC], la droite (BM) est la bissectrice intérieure issue de B si et seulement si : BA/AM = BC/CM.

(Dans le cas de la construction ci-dessous, il suffit de redéfinir I comme point quelconque de [AB] ou de la demi-droite [BA). Ce qui amène à étudier la réciproque : si la bissectrice de B coupe [AC] en M, les rapports AB/BC et AM/MC sont égaux.)

A propos de ce théorème

Démonstration 1

figmedianes
Soit D le symétrique de B par rapport à C. Le triangle ABD est isocèle en B par construction, (AC) est une de ses médianes, et le point M est donc le centre de gravité du triangle.
(BM), médiane issue de B, est un axe de symétrie du triangle, donc la bissectrice de l'angle B.

Démonstration 2

Les triangles ABM et BMC ont la même hauteur issue de B et la base AM est le double de la base MC, donc l'aire de ABM est le double de l'aire de BMC. On regarde maintenant les hauteurs issues de M de ces deux triangles et les bases BA et BC correspondantes. Comme BA est le double de BC les hauteurs sont égales, donc le point M appartient à la bissectrice de l'angle B.

Démonstration 3

Une première étape est la construction de la figure, si possible à l'aide d'un logiciel de géométrie dynamique.
La construction commence par [AM]. J milieu de [AM], C symétrique de J par rapport à M.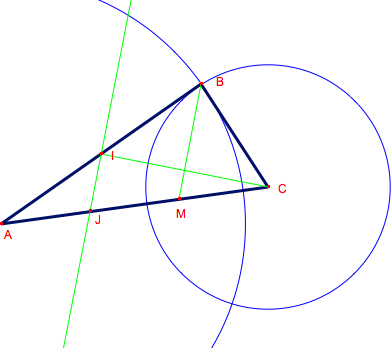
construc&
Dans le triangle BAM, on a I milieu de [AB] et J milieu de [AM], donc (IJ)// (BM).
Dans le triangle CIJ, M est le milieu de [JC], (IJ)//(BM), donc (BM) coupe [IC] en son milieu.
Dans le triangle IBC isocèle en B, (BM) est donc la médiane issue de B ...

Démonstration 4

La construction commence par [AB]. I milieu de [AB], K symétrique de I par rapport à B.
On trace les parallèles à (KC) passant par B et I.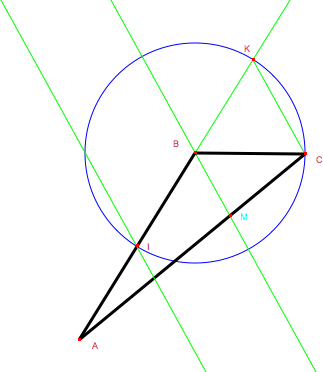
construc2
Les angles ABC et AKC interceptent l'arc IC, donc ABC = 2 AKC. D'autre part les angles AKC et ABM sont égaux comme correspondants...