PB9

irem lyon

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28
	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56

9 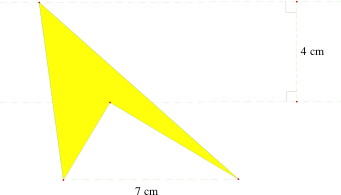Prenons de la hauteur ! Quelle est l'aire de ce quadrilatère ?	La première impression est qu'il manque une donnée. L'aire du quadrilatère est la différence des aires de deux triangles dont l'aire est variable, ou inconnue : il manque les hauteurs relatives au côté donné. Mais le calcul nécessite seulement la différence de ces hauteurs ! On peut éventuellement fournir aux élèves une figure animée, ils ont la réponse, reste alors à l'expliquer.
10 Quelle est l'aire de cette pelouse ? Le dessin ci-dessous représente une pelouse qui a la forme d'une couronne circulaire : elle est délimitée par deux cercles concentriques.	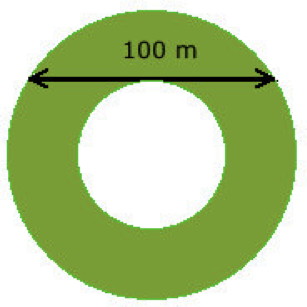Encore un problème où il semble manquer une donnée. Comme dans le précédent, l'aire cherchée est la différence de deux aires variables, celles des deux disques, que l'on n'a pas besoin de connaître, car : Pi x R² - Pi x r² = Pi x (R² - r²)