irem lyon
menu
12345678910111213141516171819202122232425262728
29303132333435363738394041424344454647484950515253 545556

44

Un billard un peu spécial

44

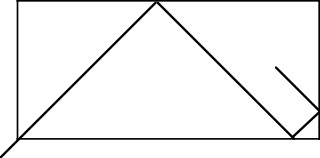
A chacun des sommets d'un billard rectangulaire, une ouverture permet d'envoyer un rayon lumineux qui se réfléchit sur les côtés du rectangle.
On se donne deux conditions supplémentaires :

1. Le billard peut être quadrillé par des carrés identiques
2. On envoie le rayon de lumière suivant la diagonale d'un carré du quadrillage. Il se réfléchit donc de la même façon.
Sa trajectoire suit toujours les diagonales du quadrillage.

Connaissant les dimensions du quadrillage, peut-on prévoir le nombre de carrés traversés par la boule ?

 		Un vrai problème de recherche qui demande du temps.
Le nombre de carrés traversés dans un quadrillage axb est égal au PPMC des entiers a et b.
Sans connaître le PPMC, les élèves peuvent trouver la formule ab/PGDC(a,b), ou des algorithmes de calcul.
Ils vont de toutes façons explorer différents cas particuliers :

pr

pr		prpr  pr
a multiple de b
Le nombre de carrés traversés est égal à a.		a et b premiers entre eux
Le nombre de carrés traversés est ab		Une piste : la similitude des figures.
On peut toujours se ramener au cas où a et b sont premiers entre eux.

Solutions et récit d'une expérimentation en classe

Thérèse Eveilleau propose sur son site une très belle animation.
Suggestion : utiliser la première animation du site après un premier temps de recherche, pour faire des essais systématiques avec les élèves, puis les laisser chercher en groupes et exposer leurs résultats. En conclusion montrer le « dépliement » du billard, qui explique la solution du PPMC .