


|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 |
51Quelles sont la ligne et la colonne de 795 471 ?  | Les lignes sont composées dans l'ordre de 1, 3, 5, 7 ... éléments, ce qui fait que les nombres en fin de ligne sont égaux à :
1, 1+3 = 4, 1+3+5 = 9 etc On peut se contenter dans ce problème de l'observation que les fins de ligne sont les carrés des entiers. Pour trouver la position de 795 471, il suffit donc de l'encadrer par deux carrés d'entiers successifs. | |||
|
* Problème annexe: La disposition des nombres en rangées de 1, 3, 5, 7, ... fait qu'en bout de ligne on a les entiers de rangs 1, 1+3, 1+3+5, etc.... Il s'agit donc de montrer que la somme des n premiers entiers impairs est un carré parfait. Quelques idées : 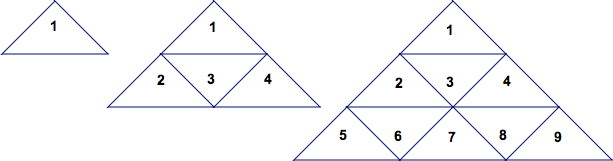 Le deuxième triangle, qui contient les deux premières lignes, est un agrandissement du premier, de coefficient 2, et ainsi de suite. Le triangle qui contient les n premières lignes est un agrandissement de coefficient n du triangle de base, donc son aire est égale à n2, ou encore il contient n2 triangles de base, donc n2 éléments.
 La somme des éléments de chaque colonne est 2n + 2. En additionnant les (n+1) éléments de chaque ligne, on a la somme S = 1 + 3 + 5 + ... + 2n+1 D'où : 2S =(n+1)(2n+2) S = (n+1)2 | ||||