irem lyon
menu
12345678910111213141516171819202122232425262728
29303132333435363738394041424344454647484950515253 545556

31

Le bon format

fig31

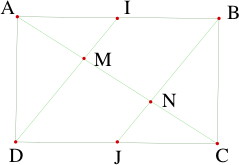
I est le milieu de AB et J le milieu de CD. Comment faut-il choisir les dimensions du rectangle ABCD pour que les angles M et N soient des angles droits ?

 Dans ce problème, c'est la conjecture qui n'est pas évidente. La condition à trouver est en effet :
AB2 = 2 BC2.
Toutes sortes de calculs sont possibles, en utilisant la trigonométrie, le calcul d'aires... mais lesquels sont éclairants ?
M est un angle droit si et si seulement les angles A et I du triangle AMI sont complémentaires, et donc si et seulement si les triangles AMI, ABC, et ADI sont semblables.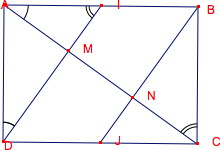

Autrement dit, la condition est que le rectangle ABCD et le rectangle "moitié" AIJD soient semblables. C'est sur cette base que sont fondés les formats normalisés bien connus A3, A4, A5...

L'utilisation d'un LGD n'apporte rien ici. En revanche, il est tout à fait pertinent de proposer aux élèves d'observer les angles M et N après pliage de rectangles de différents formats, normalisés ou non, et de chercher ensuite l'explication.

Pour des activités sur les formats de papier, voir Repères IREM n°8