6
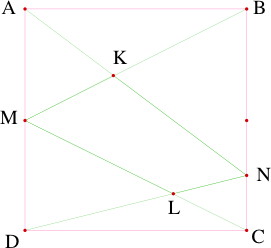
ABCD est un carré de côté 1.
M est le milieu de [AD]. N est placé au quart de [BC].
Quelle est l'aire du quadrilatère MKNL ? | L'aire du quadrilatère est 7/30.
Un problème difficile.
A l'aide du théorème de Thalès, on peut tout calculer dans cette figure, mais cela prend du temps.
Prenons pour point de départ que l'aire cherchée est égale à Aire(AND) - Aire(AMK) -Aire(MDL)
Comment calculer les aires des triangles AMK et MLD ?
Le théorème de Thalès appliqué aux triangles AKM et BKN donne que les longueurs de leurs côtés ainsi que les hauteurs issues de K sont dans le rapport 2/3, ce qui permet de calculer ces dernières :
resp 2/5 et 3/5. On en déduit l'aire de AKM : 1/10.
Un calcul analogue donne : Aire(MLD) = 1/6
L'aire du quadrilatère est 1/2-1/10-1/6.
Ce n'est pas la seule méthode, on peut aussi utiliser les deux relations :
Aire(AKB) = Aire(AMB) - Aire(AMK) = Aire( ANB)- Aire(BKN)
Aire(AMK) = Aire(BKN) x 4/9
Méthode plus lourde et sans doute moins accessible aux élèves.
Aide possible d'un LGD :
en faisant varier le côté du carré, les élèves peuvent rapidement conjecturer que l'aire de AKM est un dixième de celle du carré.
|



